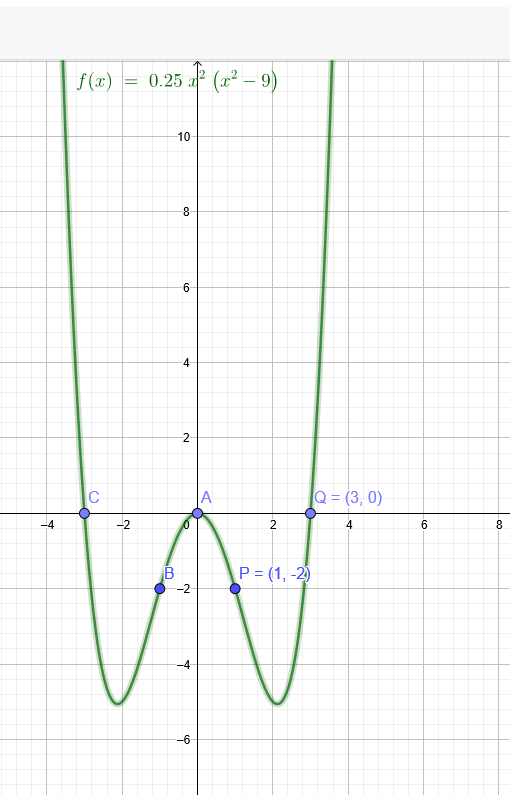
… Der Graph einer ganzrationalen Funktion 4.Grades ist achsensymmetrisch zur y Achse und geht durch den Ursprung sowie durch die Punkte P(1|-2) und Q(3|0)
Lösung mittels der Nullstellenform der Parabel 4. Grades.
Wegen der Symmetrie liegt im Ursprung eine doppelte Nullstelle:
f(x)=a*x^2*(x-3)*(x+3)=a *x^2*(x^2-9)
f(1)=a *1^2*(1^2 - 9) = - 8 a
- 8 a=-2
a=0,25
f(x)=0,25 *x^2*(x^2-9)