\(f(x)=2x^3-8x\)
Bilde zunächst die Stammfunktion
\(F(x)=\frac{1}{2}x^4-4x^2\)
Mache ein Skizze:
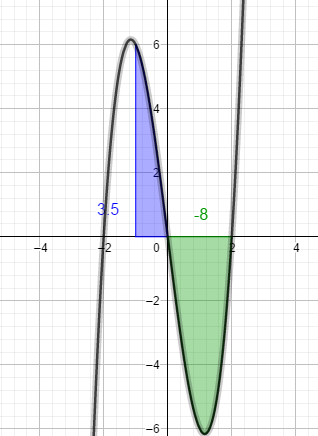
Du siehst, dass du die Flächen von -1 bis 0 und von 0 bis 2 addieren musst.
blaue Fläche
\(\int \limits_{-1}^{0}f(x)\space dx=\int \limits_{-1}^{0}2x^3-8x\space dx\\ =\bigg[\frac{1}{2}x^4-4x^2\bigg]^0_{-1}\\=\frac{1}{2}\cdot 0^4-4\cdot 0^2-\big(\frac{1}{2}\cdot (-1)^4-4\cdot (-1)^2)\\ =0-(\frac{1}{2}-4\big)=3,5\)
grüne Fläche
\(\int \limits_{0}^{2}f(x)\space dx=\int \limits_{0}^{2}2x^3-8x\space dx\\ =\bigg[\frac{1}{2}x^4-4x^2\bigg]^2_0\\=\frac{1}{2}\cdot 2^4-4\cdot 2^2-0\\ =8-16=-8\). Der Betrag davon ist \( 8\).