Hallo
Normalparabel y=x^2
a) nach oben um a verschieben: jeder Wert wird a größer, deshalb jetzt y=x^2+a
a negativ nach unten verschoben
b) in y Richtung strecken um den Faktor b: jeder Wert wird b mal so groß (oder mit b <1) so klein also x=b*x^2
strecken und nach oben schieben: y=ax^2+b
c in x Richtung um c verschieben ist etwas schwerer zu verstehen . Siehe meine Graphik die rote Parabel ist um 3 nach rechts verschoben. wenn ich den Wert an der Stelle x=4 wissen will gehe ich 3 nach links und lese dort den Wert ab, also (4-3)^2, der Wert bei 5 ist (5-3)^2
der Wert bei irgendeinem x ist (x-3)^2
deshalb hat die um 3 nach rechts verschobene Parabel die Gleichung y=(x-3)^2
so jetzt bist du dran, zu sagen was du davon verstehst , und was nicht-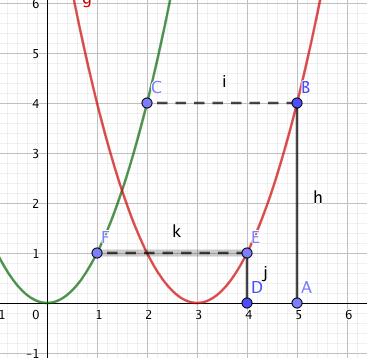
Gruß lul