Begründen Sie Ihre Entscheidungen.

Question

Aufgabe:

h ist eine für ∈ R differenzierbare Funktion.
Nebenstehend ist für −1,5 ≤ ≤ 3 das Schaubild ihrer Ableitungsfunktion h ́() dargestellt. Entscheiden Sie, ob folgende Aussagenüber die Funktion h richtig, falsch oder unentscheidbar sind. Begründen Sie Ihre Entscheidungen.
(1) An der Stelle = −1 hat das Schaubild von h einen Tiefpunkt.
(2) h() >0für0 ≤ ≤ 3.
(3) An der Stelle = 0 hat der Graph von h eine Tangente, die parallel ist zur
Geraden mit der Gleichung ! = − 7.
(4) h ist streng monoton wachsend für −1,5 ≤ ≤ 0 .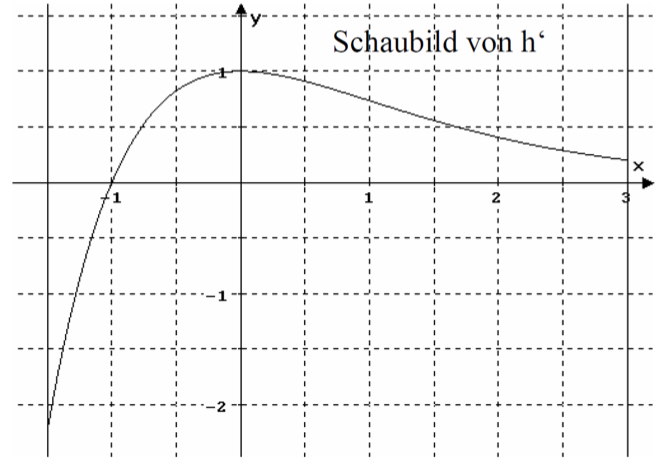

Problem/Ansatz:

Hallo

Die Aufgabe 1 konnte ich schon lösen. Aber ich weiß nicht wie ich die anderen lösen soll.

Wie geht man da vor ? Was ist die Erklärung für die Aufgaben?

Ich bitte um Hilfe

Answer 1

(1) An der Stelle = −1 hat das Schaubild von h
einen Tiefpunkt.
Die Steigung an der Stelle x = -1 ist null
Die Steigung ändert sich dort von negativ ( fallend )
nach positiv ( steigend ).
Die Stelle ist ein Tiefpunkt von h.

(2)(3)(4)  berichtige erst einmal die Fragen.

Comments

Oh das ist mir entgangen. Entschuldigung!

(2) h() > 0 für 0 ≤ ≤ 3.
(3) An der Stelle = 0 hat der Graph von h eine Tangente, die parallel ist zur Geraden mit der Gleichung t= − 7.

(4) h ist streng monoton wachsend für −1,5 ≤ ≤ 0 .

---

2) h(x) > 0 für 0 ≤ x ≤ 3.

(3) An der Stelle x = 0 hat der Graph von h eine Tangente, die parallel ist zur Geraden mit der Gleichung yt= x-7.

(4) h ist streng monoton wachsend für −1,5 ≤ x≤ 0 .

Irgendwie verschwindet das x immer

Sorry !

---

2) h(x) > 0 für 0 ≤ x ≤ 3.
h ( 0 ) = 1
h ( 3 ) = 0.2 ( geschätzt )

(3) An der Stelle x = 0 hat der Graph von h eine Tangente, die parallel ist zur Geraden
mit der Gleichung yt= x-7.
Was soll das t in der Gleichung ?
Ist wohl zu viel.
Tangentengleichung
b ( x ) = 1

(4) h ist streng monoton wachsend für −1,5 ≤ x≤ 0
Steigung ist negativ
-1.5 .. 0 = fallend