Zwölfeck Kante berechnen

Question

Ein regelmäßiges Zwölfeck ist von einem Kreis mit dem Durchmesser d=20cm umschrieben.

a) Berchne die Kantenlänge des Zwölfecks!

b) Bestimme die restliche Fläche des Kreises!


Kann mir das jemand erklären bzw. zeigen ich finde nämlich keine formel über ein Zwölfeck ?

Comments

Mach Dir eine Skizze. Dann siehst Du, dass Du 12 gleichschenklige Dreiecke hast, über die Du Aussagen treffen kannst, da der Durchmesser gegeben ist.

Vllt schaffst Du es damit selbst, bis jemand eine Antwort gibt?! :)

---

Ich komme trotzde nicht darauf ?

---

a) habe ich aber b) blick ich nicht kann mir bitte jemand helfen :)

Answer 1

Hi,

wenn Du mir meine zeichnerischen Fähigkeiten nicht übel nimmst, dann versuche ich mich mal ;).

 

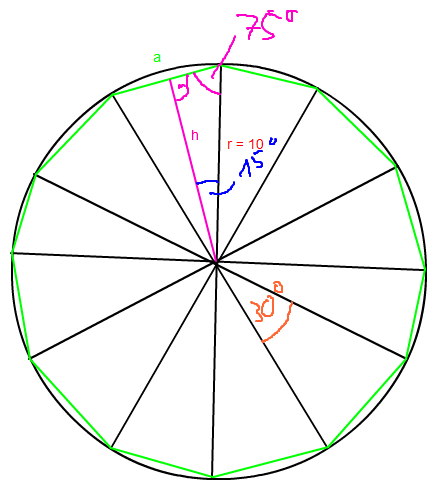
Augenmerk lege auf obiges Dreieck. Das hat die Schenkellänge von 10 cm.

Jede Speiche hat 30°, denn es ist ja ein Kreis (360°) welcher in 12 Teile zerschnitten wird: 360°/12 = 30°.

Die Hälfte eines Dreiecks hat also 15°.

Damit können wir h errechnen!

cos(15°) = h/10

h = 10*cos(15°) = 9,659

Jetzt noch a/2 berechnen:

sin(15°) = (a/2)/10

(a/2) = 10sin(15°) = 2,588

Damit hat a eine Länge von a = 5,176 cm.

 

b)

Der Flächeninhalt eines (Zwölftel-)Dreiecks berechnet sich zu A = 1/2*a*h = (a/2)*h = 25 cm^2

 

Insgesamt haben wir also einen Flächeninhalt von A_12-Eck = 12*25 cm^2 = 300 cm^2

 

Flächeninhalt des Kreises:

A_Kreis = πd^2/4 = 314,159 cm^2

 

Die Restfläche ist also A_Rest =  A_Kreis - A_12Eck = 314,159 cm^2 - 300 cm^2 = 14,159 cm^2.

 

Alles klar?

Grüße

Comments

Danke das du dir die mühe gemacht hast :)

---

Gerne :). Hat Spaß gemacht, obwohl ich normal kein Freund der Geometrie bin^^.