berechne die Kantenlänge und die länge einer Flächendiagonale eines Würfels , dessen Raumdiagonale 8cm lang ist.

Question

Aufgabe:

berechne die Kantenlänge und die länge einer Flächendiagonale eines Würfels , dessen Raumdiagonale 8cm lang ist.

Problem/Ansatz:

ich komme bei dieser Aufgabe nicht weiter und gehe in die neunte lasse. danke im voraus!

Answer 1

Zwei Kanten \(a\) und Flächendiagonale \(d_2\) bilden ein rechtwinkliges Dreieck mit Hypotenuse \(d_2\). Pythagoras meint dazu

        \(a^2 +a^2 = d_2^2\).

Raumdiagonale \(d_3\), Flächendigonale \(d_2\) und Kante \(a\) bilden ein rechtwinkliges Dreieck mit Hpothenuse \(d_3\). Pythagoras meint dazu

    \(d_2^2 +a^2 = d_3^2\).

Setze die bekannten Angaben ein und löse das Gleichungssystem.

Answer 2

Hallo

zeichne einen Würfel mit der Kantenlänge a. hab ich für dich gemacht!

dann bestimme mit Pythagoras die Länge einer Flächendiagonale: (schwarz)

d^2=a^2+a^2, die Raumdiagonale (rot) 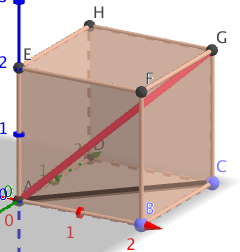 ist jetzt Hypotenuse in dem rechtwinkligen Dreieck mit Katheten a und d , ihre Länge sei D

dann hast du D^2=d^2+a^2=..... jetzt kennst du D^2 kannst daraus also a^2 und damit a bestimmen.

Gruß lul