Gegeben seien ein sinkender Badegast und ein Rettungsschwimmer. Der Schwimmer will den Badegast retten. Er kann mit Geschwindigkeit \( v_{r} \) rennen und mit Geschwindigkeit \( v_{s} \) schwimmen. Zeigen Sie. dass die schnellstmögliche Strecke des Retters durch \( \frac{\sin \left(\varphi_{r}\right)}{\sin \left(\varphi_{x}\right)}=\frac{v_{r}}{v_{s}} \) gegeben ist, wobei die Winkel \( \varphi_{r} \) und \( \varphi_{s} \) der Skizze zu entnehmen sind.
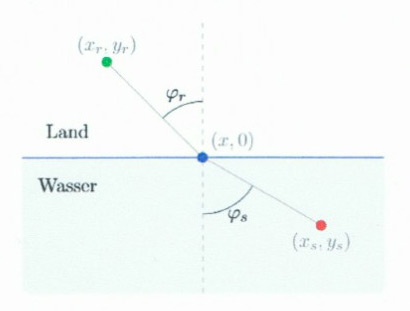
Bemerkung: Das Snelliussche Brechungsgesetz besagt \( \frac{\sin \left(\varphi_{r}\right)}{\sin \left(\varphi_{s}\right)}=\frac{n_{n}}{n_{r}} \), da die Brechungsindices \( n \) antiproportional zu den Geschwindigkeiten \( v \) sind. Das Licht bewegt sich also so, dass die Lichtlaufzeit minimal ist.