Wie kann ich das mit der "großen Lösungsformel" berechnen?

Question

3.14 c) 5x²-4x-33=0

Wie kann ich das mit der "großen Lösungsformel" berechnen?

Answer 1

Indem du in die "große Lösungsformel" a=5,b=-4 und c=-33 einsetzt. Nach Umwandlung in  x²-0,8x-6,6=0 genügt auch die pq-Formel mit p=-0,8 und q=-6,6.

Comments

Ich habe x=4±√4²-4×5×(-33)/2×5= 4±√26/10 gerechnet aber ich komme nicht mehr weiter.

Wie kann ich es auf dieser Weise rechnen?

---

Weiter kommst du jetzt nur noch mit dem Taschenrechner. Da darf keine Wurzel aus einer negativen Zahl stehen, Ergebnis; x_1/2=0,8±√7,24≈0,8±2,7.

---

Wenn ich es im Taschenrechner eingebe kommt x=0,91 und x=-0,11 das ist aber falsch es sollte x= -11/5 und x=3 herauskommen.

---

Deine Zwischenergebnisse sind schon falsch.

---

Welche Zwischenergebnisse sind falsch?

Answer 2

Hallo,

y= a x^2 +bx +c

große Lösungsformel: \( x_{1,2}=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \)

\( a= \) Wert des ersten Glieds, \( b \) =Wert des zweiten Glieds, \( c \) =Wert des dritten Glieds

a= 5

b=-4

c= -33

---->

x_1.2=(4± √(16+660))/10 = (4±  26)/10

x₁= 3

x₂= -11/5

Comments

Warum haben Sie hier x_{1.2}=(4± √(16+660))/10 geschrieben und nicht

x_{1.2}=(4± √(16-660))/10

---

-4ac=  - 4 *5 *(-33)= 20*33= 660  (Minus mal Minus ergibt Plus)

Answer 3

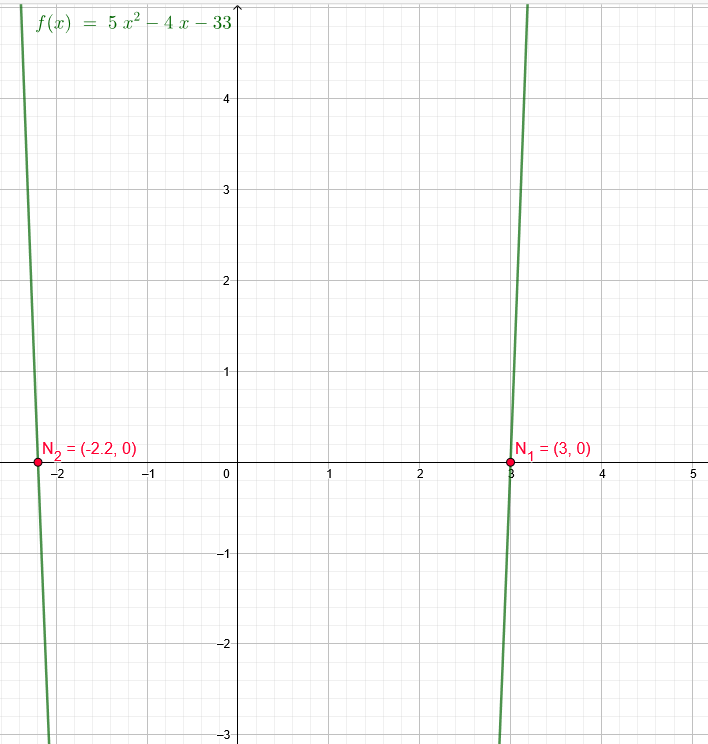
Ich zeige dir den Weg über die quadratische Ergänzung (q.E.)

5x²-4x-33=0|+33

5x²-4x=33|:5

x²-\( \frac{4}{5} \) x=\( \frac{33}{5} \) | + q.E.( \( \frac{-2}{5} \))^2  =\( \frac{4}{25} \)

x²-\( \frac{4}{5} \) x+\( \frac{4}{25} \)=\( \frac{33}{5} \)+\( \frac{4}{25} \)

(x - \( \frac{2}{5} \))^2 =\( \frac{169}{25} \)|\( \sqrt{} \)

x₁= \( \frac{2}{5} \)+\( \frac{13}{5} \)=3

x₂= \( \frac{2}{5} \)-\( \frac{13}{5} \)= -\( \frac{11}{5} \)