Aufgabe:
Text erkannt:
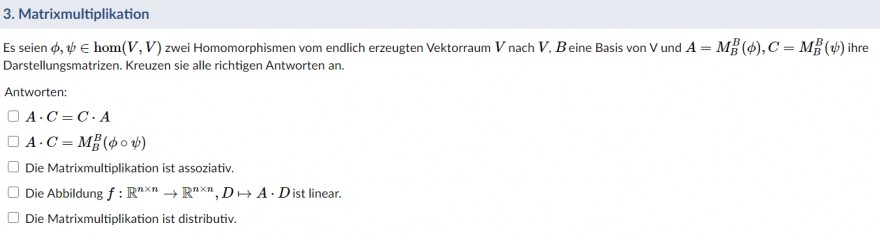
3. Matrixmultiplikation
Es seien \( \phi, \psi \in \operatorname{hom}(V, V) \) zwei Homomorphismen vom endlich erzeugten Vektorraum \( V \) nach \( V, B \) eine Basis von \( V \) und \( A=M_{B}^{B}(\phi), C=M_{B}^{B}(\psi) \) ihre Darstellungsmatrizen. Kreuzen sie alle richtigen Antworten an.
Antworten:
\( A \cdot C=C \cdot A \)
( A \cdot C=M_{B}^{B}(\phi \circ \psi) \)
Die Matrixmultiplikation ist assoziativ.
Die Abbildung \( f: \mathbb{R}^{n \times n} \rightarrow \mathbb{R}^{n \times n}, D \mapsto A \cdot D \) ist linear.
Die Matrixmultiplikation ist distributiv.
Problem/Ansatz: