Aufgabe:
Durch die Einnahme eines Medikamentes zum Zeitpunkt t=0 gelangt ein bestimmter Wirkstoff in das Blut
des Patienten. Die Wirkstoffkonzentration, die zum Zeitpunkt te [0; 24) im Körper des Patienten ist ann durch eine Funktion der Funktionenschar f(t) = 20*t*e^-k*t mit k> 0, beschrieben werden
Dabei wird die Zeit t in Stunden und die Wirkstoffkonzentration in mg/l angegeben.
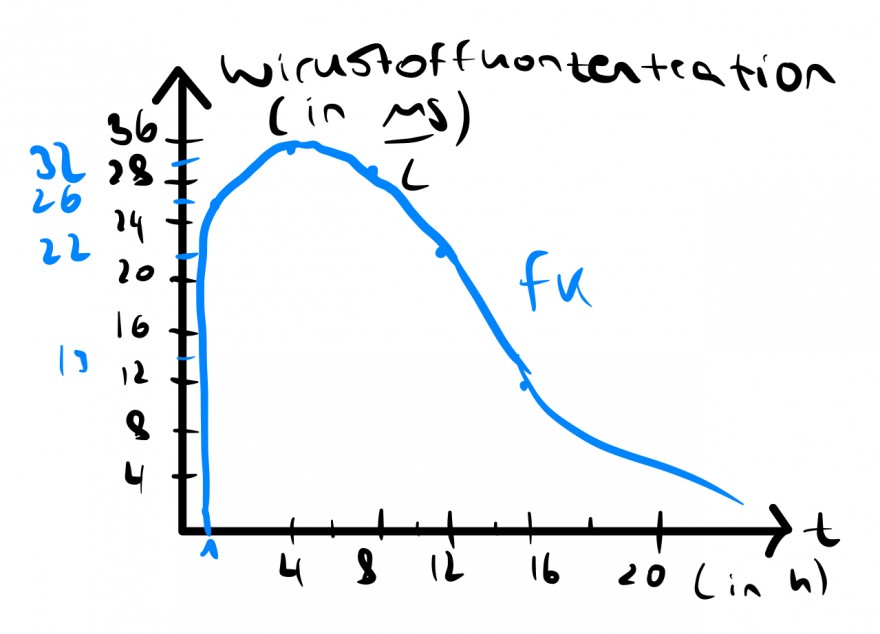
5.1 Die nebenstehende Abbildung zeigt einen zeitlichen Verlauf, bei dem die Wirkstoffkonzentration im Blut des Patienten zwe Stunden nach der Einnahme des Medikamentes 26,813mg/l beträgt.
a) Berechnen Sie den Parameter k der Funktion f, die den zeitlichen Verlauf der Wirkstoffkonzentration modelhaft
angegeben. Wirkstoffkonzentration beschreibt, sowie die Höhe der Wirkstoffkonzentration 12
Stunden nach der Einnahme des Medikamentes.
Ergebnis: k ≈ 0,2
b) Berechnen Sie den Zeitpunkt und den Wert der maximalen
Konzentration des Wirkstoffes im Blut
Problem/Ansatz:
Die Aufgabe soll mit dem GTR gelöst werden. Nur erhalte ich nicht den korrekten Graphen wenn ich f(t) = 20*t*e^-k*t so im Grafikfenster eingebe.
Bei Aufgabe b) hatte ich mir gedacht, dass ich den Hochpunkt angebe, allerdings kommen Werte raus, die nicht stimmen können.
Lieben Dank!