Aufgabe Medikamenteneinnahme:
Durch die Einnahme eines Medikamentes zum Zeitpunkt \( t=0 \) gelangt ein bestimmter Wirkstoff in das Blut des Patienten. Die Wirkstoffkonzentration, die zum Zeitpunkt \( t \in [0; 24] \) im Körper des Patienten ist, kann durch eine Funktion der Funktionenschar \( f_{k}(t)=20 \cdot t \cdot e^{-k \cdot t} \) mit \( k>0 \), beschrieben werden.
Dabei wird die Zeit \( \mathrm{t} \) in Stunden und die Wirkstoffkonzentration in \( \frac{\mathrm{mg}}{\mathrm{I}} \) angegeben.
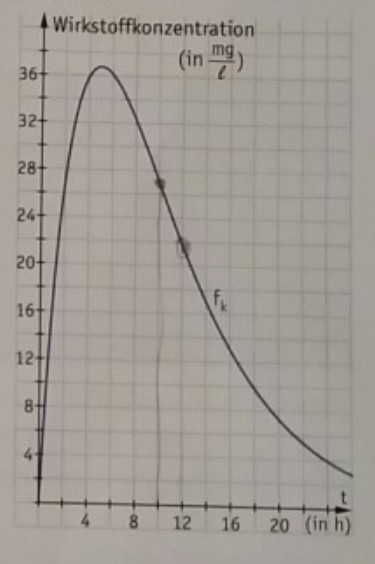
5.1 Die nebenstehende Abbildung zeigt einen zeitlichen Verlauf, bei dem die Stunden nach der Einnahme des Medikamentes \( 26,813 \frac{\mathrm{mg}}{\mathrm{I}} \) beträgt.
a) Berechnen Sie den Parameter \( k \) der Funktion \( f_{k} \), die den zeitlichen Verlauf der Wirkstoffkonzentration modellhaft beschreibt, sowie die Höhe der Wirkstoffkonzentration 12 Stunden nach der Einnahme des Medikamentes. Ergebnis: \( k \approx 0,2 \)
b) Berechnen Sie den Zeitpunkt und den Wert der maximalen Konzentration des Wirkstoffes im Blut.
c) Weisen Sie nach, dass, die Wirkstoffkonzentration nach 24 Stunden kleiner als \( 4 \frac{\mathrm{mg}}{\mathrm{l}} \) ist.
d) Berechnen Sie den Zeitpunkt, an dem die Wirkstoffkonzentration am stärksten abnimmt.
5.2 Untersuchen Sie das Verhalten der Funktion \( \mathrm{f}_{0,2} \) für \( \mathrm{t} \rightarrow \infty \).
Interpretieren Sie das Ergebnis im Hinblick auf einen langfristigen Abbau des Wirkstoffes.
5.3 Berechnen Sie für \( k>0 \) die Extrempunkte der Funktionenschar \( f_{k} \) sowie eine Gleichung der Ortslinie der Extrempunkte.
5.4 Durch eine entsprechende Dosierung der Einnahmemenge kann man den Parameter k beeinflussen. Innerhalb welcher Grenzen muss \( k \) liegen, damit die maximale Wirkstoffkonzentration \( 50 \frac{\mathrm{mg}}{\mathrm{l}} \) nicht übersteigt?
Ansatz/Problem:
Also ich hab berechnet, bin mir aber bei 5.4 nicht sicher weil ich nur einen Wert für k habe und nicht weiß wie ich damit die Grenzen angeben soll. Mein Ergebnis: k = 1/(2,5e).