Differenzialrechnung Extrempunkte Monotonie und Krümmungsintervalle

Question

Aufgabe: Bestimmen Sie die Extrempunkte und erläutern Sie die einzelnen Monotonie und Krümmungsintervalle.

Kann mir bitte jemand sagen ob ich da richtig vorgehe und wie ich weiter machen sollte

d) f(x) = 0,25x^4-3x^3+9x^2

f'(x) = x^3-9x^2+18x

f''(x) = 3x^2-18x+18=0 | :3

x^2-6x+6=0

PQ Formel da kommt bei mir wurzel 3 raus und als Ergebnis habe ich

x1= 3+ wurzel 3 und

x2 = wurzel 3 raus kann das stimmen ?

Und wenn ich es in die zweite Ableitung einsetze bekomme ich einmal -24+ wurzel 3 raus und einmal 27-18 wurzel 3

Problem/Ansatz:

Comments

Nein ich habe meinen Fehler entdeckt

f(x) = 0,25x4-3x3+9x2

f'(x) = x3-9x2+18x

x(x^2-9x+18)

Da hat man schon mal eine x=0

Dann PQ Formel

Lösung x1 = 6 und x2 = 3

Dann die zweite Ableitung

f''(x) = 3x^2-18x+18=0 einsetzen

f'' (6) = 3*6^2-18*6+18 = 18

f'' (3) = 3*3^2-18*3+18 = -9

Answer 1

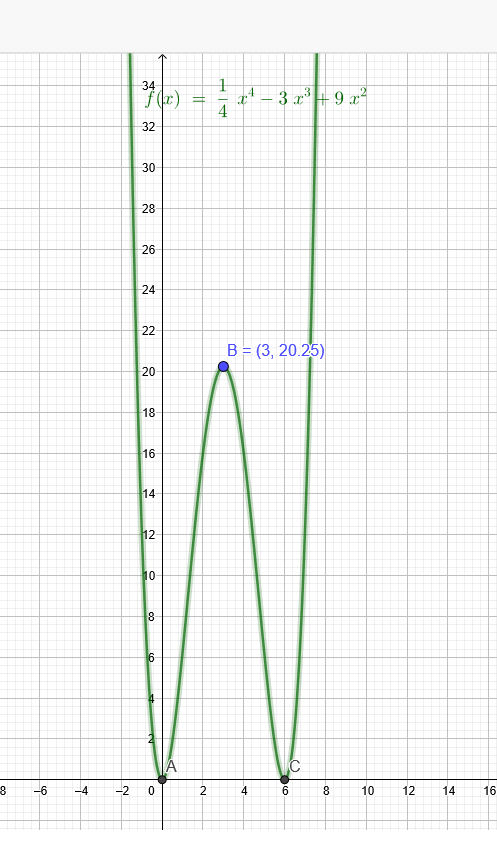
f(x) = 0,25x^4-3x^3+9x^2

f´(x) =x^3-9x^2+18x

f´´(x)=3x^2-18x+18

x^3-9x^2+18x=0

x*(x^2-9x+18)=0

x₁=0  →   f(0) =0

x^2-9x+18=0

x^2-9x=-18

(x-\( \frac{9}{2} \))^2=-18+4,5^2=2,25|\( \sqrt{} \)

x₂=\( \frac{9}{2} \)+1,5=6 →f(6) = 0,25*6^4-3*6^3+9*6^2 =0

x₃=\( \frac{9}{2} \)-1,5=3 →f(3) = 0,25*3^4-3*3^3+9*3^2 =20,25

Art der Extremwerte:

f´´(0)=18>0 → Minimum

f´´(3)=3*3^2-18*3+18   = -9 <0   → Maximum

f´´(6)=3*6^2-18*6+18  = 18  > 0 → Minimum

Text erkannt:

1