Im Koordinatensystem:
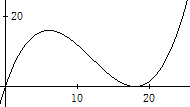
f(t) = 1/54· t 3 — 2/3· t2 + 6 t
Stellen sie die Gleichung der Wendetangente auf
f ''(t)=t/9-4/3
0=t/9-4/3 daher t=12 und f(12)=8.
f '(12)=-2.
Punkt-Steigungs-Form: -2=\( \frac{y-8}{x-12} \).
Berechnen sie den Zeitpunkt, zu dem Wirkstoff vollständig ausgeschieden ist.
0=1/54· t 3 — 2/3· t2 + 6 t
0=t·(1/54· t2 — 2/3· t + 6)
t1=0 oder 1/54· t2 — 2/3· t + 6=0 |·54
t2-36t+324=0
t2=18.