Skizzieren Sie den Graphen einer Funktion f

Question

Aufgabe:

Skizzieren Sie den Graphen einer Funktion f, welche die folgenden Bedingungen erfüllt.

a) Der Graph von f ist rechtsgekrümmt und besitzt keinen Wendepunkt.

b) Dei Ableitungen f´ und f´´ haben nur negative Funktionswerte

Answer 1

a) Der Graph von f ist rechtsgekrümmt und besitzt keinen Wendepunkt.

f(x)=\( \frac{1}{2} \) *(x-3)^2+4

b)  Die Ableitungen f´ und f´´ haben nur negative Funktionswerte

f´´(x)=-x+5    →   f´(x)=\( \int\limits_{}^{} \)(-x+5)*dx=0,5x^2+5x+C_1  → f(x) =\( \int\limits_{}^{} \)(0,5x^2+5x+C_1)*dx =\( \frac{1}{6} \)x^3+\( \frac{5}{2} \)x^2+C_1*x+C_2

Es sei nun C_1=2 und C_2=-\( \frac{1}{2} \)

f(x)=\( \frac{1}{6} \)x^3+\( \frac{5}{2} \)x^2+2*x-\( \frac{1}{2} \)

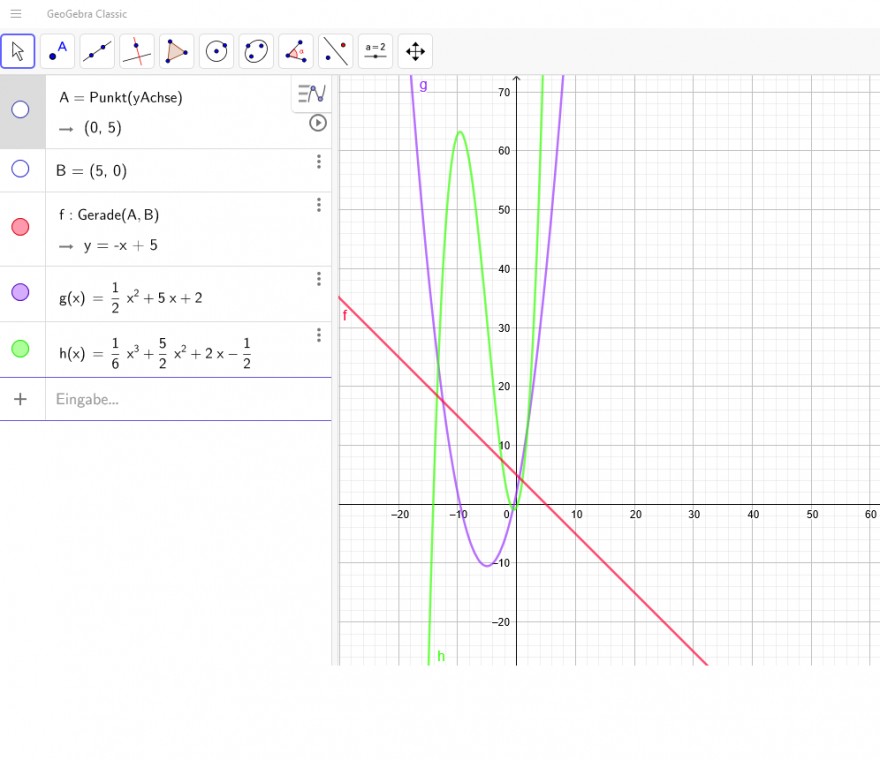
Text erkannt:

GeoGebra Classicic
\( \mathrm{A}= \) Punkt(yAchse)
\( \rightarrow(0,5) \)
\( B=(5,0) \)
\( f: \operatorname{Gerade}(A, B) \)
\( \rightarrow y=-x+5 \)
\( h(x)=\frac{1}{6} x^{3}+\frac{5}{2} x^{2}+2 x-\frac{1}{2} \)

Comments

Achtung: ich bin von einer falschen 2.Ableitung ausgegangen.

Versuche mal meinen Weg mit f´´(x)= -  3.

---

Achte aber bei der Wahl von C_1 und C_2, dass du mit den Funktionswerten im negativen Bereich bleibst.

Answer 2

a)  z.B. f(x) = -x^2

b) f(x) = 1/x über dem Intervall [-6; -0,2 ]

Answer 3

a) jede nach oben geöffnete Parabel

b) z.B. -e^x