Hallo,
vielleicht kann mir hier ja jemand helfen, stecke leider seit fast 2 Tagen bei folgender Aufgabe fest.
Zur Erläuterung:
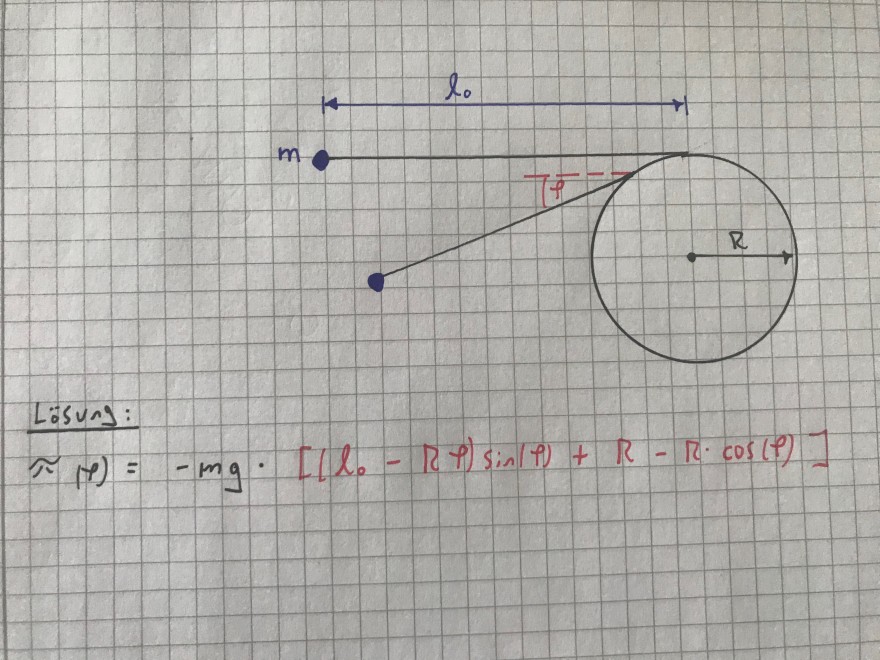
Ich habe eine festsitzende unbewegliche Scheibe. Oben an der Scheibe ist ein undehnbares Seil befestigt mit der Ausgangslänge l_0. Am Ende des Seils ist wiederum ein Massenpunkt befestigt.
Das Seil wird nun (wie in der Skizze dargestellt) um den Winkel Phi über die Scheibe gelegt. Meine Aufgabe ist es, für die potentielle Energie die y-Koordinate des Massenpunktes zu bestimmen (in Abhängigkeit vom Winkel Phi).
Als Lösung soll rauskommen:
[(l0 - R * Phi) sin(phi) + R - R * cos(phi)] = y
Ich habe jedoch Schwierigkeiten diese Lösung nachzuvollziehen, bzw. wie diese Zustande kommt. Vor allem den Teil R*Phi*sin(Phi). Was wurde damit berechnet, wo kommt das her?
Text erkannt:
L:ssung:
\( -(P) \sin \mid \varphi)+R-R \)
\( \pi(p)=-m g \).
Würde mich freuen, wenn mir das jemand erklären könnte.
mfg