Hallo, ich hoffe ich bin nicht zu spät
Rechnung: Ist es mindestens eins, ziehst Du die Gegenwahrscheinlichkeit, nämlich fünf Nieten, von 1 ab:
1-[(20 über 0)*(80 über 5)]/(100 über 5)=68,1%
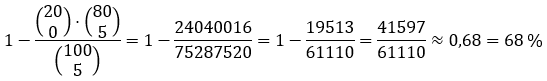
[Es gibt insgesamt binomial(100, 5) Möglichkeiten 5 Lose aus den 100 Losen auszuwählen. Dabei gibt es binomial(20, 1)*binomial(80, 4) Möglichkeiten 1 Los aus den 20 Gewinnerlosen und die anderen 5 - 1 = 4 Lose aus den 100 - 20 = 80 anderen Losen zu ziehen.]

Die Wahrscheinlichkeit, dass darunter mindestens ein Gewinnlos ist (Das von oben)