Aloha :)
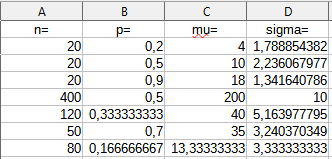
Der Erwartungsert ist \(\mu=n\cdot p\).
Die Standardabweichung ist: \(\sigma=\sqrt{n\cdot p\cdot(1-p)}=\sqrt{\mu\cdot(1-p)}\).
Mit diesen beiden Formeln kannst du alles ausrechnen. Nur die letzte Aufgabe nicht, das ist nur \(n\) gegeben, sodass das Ergebnis unbestimmt ist. Bei der vorletzten Aufgabe hast du \(p\) und \(\sigma\) gegeben, die ist noch interessant. Dafür brauchst du die Umformung:$$\sigma=\sqrt{\mu\cdot(1-p)}=\sqrt\mu\cdot\sqrt{1-p}\implies\mu=\frac{\sigma^2}{1-p}$$