Aufgabe:
In einem Unternehmen wird ein Produkt gefertigt, dass in 3 Unterbaugruppen aufgeteilt ist, welche schließlich in die Hauptmontage integriert werden.
Eine der Unterbaugruppen dauert im Durchschnitt 31,5 Minuten.
Peter denkt, er kann die Taktzeit des Prozesses senken. Dazu führt er einen Hypothesentest durch.
Er zeichnet die Zykluszeit für 12 Unterbaugruppen mit 3 Kollegen auf, von denen jeder den Vorgang 4 mal durchführt.
Die Messwerte sind wie folgt:
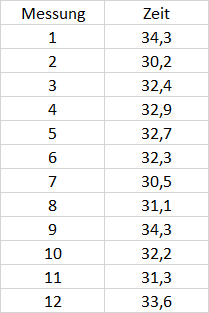
a) Peter möchte den Mittelwert berechnen, der im 98%tigen Konfidenzintervall liegt
Nennen Sie die obere und untere Grenze des Intervalls.
b) Nennen Sie den Wert der Teststatistik T(x)
Problem/Ansatz:
Mittelwert (gemessen): 32,32
Standardabweichung: 1,35903
Warscheinlichkeit: 0,98
Alpha: 0,02
alpha/2: 0,01
Z(C)= 2,328
(bei Z bin ich mir unsicher, meiner Meinung nach handelt es sich um eine T Verteilung, weil n < 30 und es ist ein einseitiger Test weil wir messen möchten, ob der beobachtete Wert sich verringert hat ist)
a) Konfidenzintervall:
Obere Grenze: 31,4
Untere Grenze: 33,23
b) T(x)
(32,32-31,5)/(1,35903)/Wurzel(12)=2,081639
(Mittelwert "neu"-Mittelwert "alt")/(Standardabweichung/Wurzel(n))
Ich bin mir völlig unsicher bei "a", da ich nicht weiß, wie man Z(C) korrekt berechnet. Da verhau ich mich oft. Liege ich dieses mal richtig?