Text erkannt:
Berechnen Sie mithilfe von Stammfunktionen den Inhalt der markierten Fläche.
\( f(x)=e^{x}-x \)
\( g(x)=1 \)
Zur Vereinfachung verschiebe ich beide Graphen um eine Einheit nach unten:
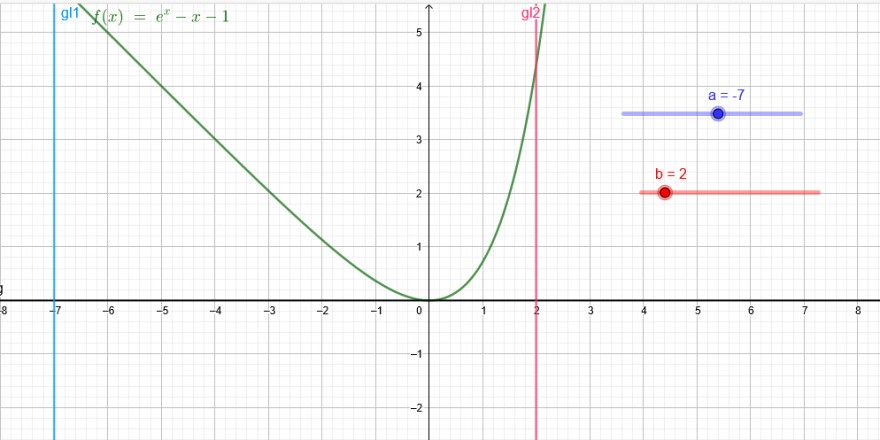
\( f_{1}(x)=e^{x}-x-1 \)
\( g_{1}(x)=0 \)
Untere Grenze a mit \( a<0 \) und \( b>0 \rightarrow \rightarrow[ \) mit der Annahme, dass sich die markierten Flächen so darstellen]
$$ A=\int \limits_{a}^{b}\left(e^{x}-x-1\right) \cdot d x=\left[e^{x}-\frac{1}{2} x^{2}-x\right]_{a}^{b}=\left[e^{b}-\frac{1}{2} \cdot b^{2}-b\right]-\left[e^{a}-\frac{1}{2} a^{2}-a\right] $$
Mit \( a=-7 \) und \( b=2 \) ergibt das
$$ A=\left[e^{2}-\frac{1}{2} \cdot 2^{2}-2\right]-\left[e^{-7}-\frac{1}{2} \cdot(-7)^{2}-(-7)\right] \approx 20,88 F E $$