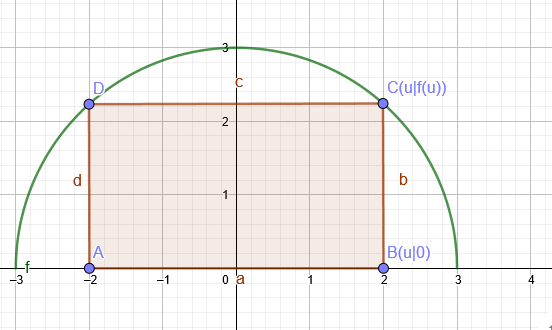
Aufgabe: Wie muss in einem Halbkreis (Radius r) das eingeschriebene Rechteck mit den Seiten x und y gewählt werden, damit die Fläche F=x*y maximal wird?
A(u)=2*u*f(u) soll maximal werden
f(x) = \( \sqrt{r^2-x^2} \)
f(u) = \( \sqrt{r^2-u^2} \)
A(u)=2*u*\( \sqrt{r^2-u^2} \)=\( \sqrt{4u^2*(r^2-u^2)} \)=\( \sqrt{4u^2*r^2-4u^4} \)
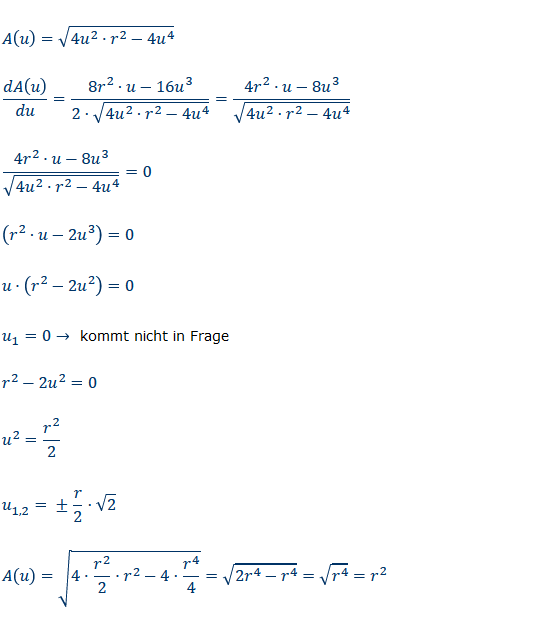
Text erkannt:
\( A(u)=\sqrt{4 u^{2} \cdot r^{2}-4 u^{4}} \)
\( \frac{d A(u)}{d u}=\frac{8 r^{2} \cdot u-16 u^{3}}{2 \cdot \sqrt{4 u^{2} \cdot r^{2}-4 u^{4}}}=\frac{4 r^{2} \cdot u-8 u^{3}}{\sqrt{4 u^{2} \cdot r^{2}-4 u^{4}}} \)
\( \frac{4 r^{2} \cdot u-8 u^{3}}{\sqrt{4 u^{2} \cdot r^{2}-4 u^{4}}}=0 \)
\( \left(r^{2} \cdot u-2 u^{3}\right)=0 \)
\( u \cdot\left(r^{2}-2 u^{2}\right)=0 \)
\( u_{1}=0 \rightarrow \) kommt nicht in Frage
\( r^{2}-2 u^{2}=0 \)
\( u^{2}=\frac{r^{2}}{2} \)
\( u_{1,2}=\pm \frac{r}{2} \cdot \sqrt{2} \)
\( A(u)=\sqrt{4 \cdot \frac{r^{2}}{2} \cdot r^{2}-4 \cdot \frac{r^{4}}{4}}=\sqrt{2 r^{4}-r^{4}}=\sqrt{r^{4}}=r^{2} \)