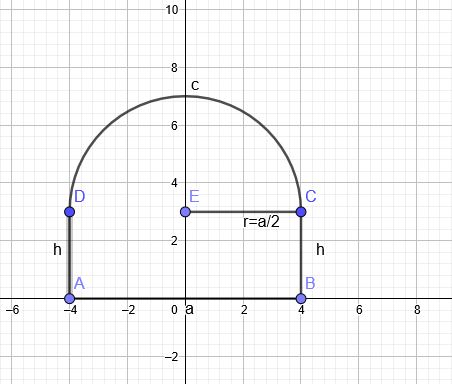
\(A(a,h)=a\cdot h+\frac{1}{2}\cdot(\frac{a}{2})^2\cdot π\) soll maximal werden.
NB:
\(10=a+h+ \frac{a}{2} \cdot π+h=a+2h+ \frac{a}{2} \cdot π\)
Nach \(h\) auflösen:
\(2h=10-a-\frac{a}{2} \cdot π\)
\(h=5-\frac{a}{2}-\frac{a}{4} \cdot π\)
\(A(a)=a\cdot (5-\frac{a}{2}-\frac{a}{4} \cdot π)+\frac{a^2}{8}\cdot π\)
\(A(a)= (5a-\frac{a^2}{2}-\frac{a^2}{4} \cdot π)+\frac{a^2}{8}\cdot π\)
\(A(a)= 5a-\frac{a^2}{2}-\frac{a^2}{8}\cdot π\)
\( \frac{dA(a)}{da}=5-2a-\frac{a}{4}\cdot π\)
\( 5-2a-\frac{a}{4}\cdot π=0\)
\(a=\frac{20}{8+π}\)
\(h=...\)
\(A=...\)