Berechne die Höhe h, einer Seitenfläche, die Körperhöhe h und den Oberflächeninhalt O der Pyramide.

Question

Aufgabe:

a. Bei einer Pyramide mit quadratischer Grundfläche (quadratische Pyramide) ist a= 15 cm und die Seitenkante s=20 cm lang. Berechne die Höhe h, einer Seitenfläche, die Körperhöhe h und den Oberflächeninhalt O der Pyramide. die Grundkante b. Bei einer quadratischen Pyramide ist die Grundkante 40 m lang, die Körperhöhe beträgt 30 m. Berechne die Höhe h, einer Seitenfläche sowie die Länge s der Seitenkanten.

Answer 1

Seien A,B die Enden einer Grundseite, M der Mittelpunkt dieser Grundseite, F der Fußpunkt der Höhe der Pyramide und S die Spitze der Pyramide.

Dann gibt es die rechtwinkligen Dreiecke AMS und FMS.

a= 15 cm und die Seitenkante s=20 cm

Berechne daraus mit Pathagoras in einem der obigen Dreiecke die Höhe einer Seitenfläche.

Mit dem Ergebnis und dem anderen Dreieck kannst du dann die Höhe der Pyramide berechnen.

Answer 2

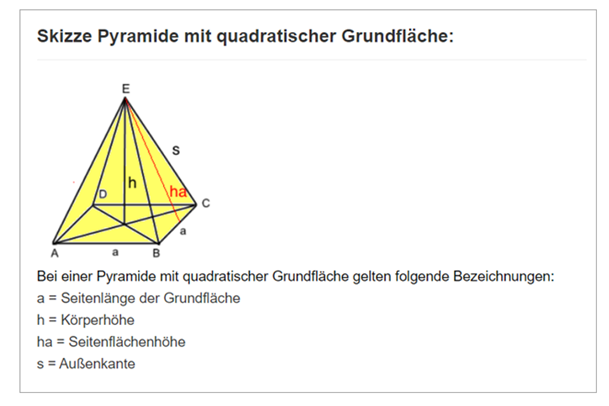
Gegeben:

a=15 cm
s= 20

Gesucht: Höhe Pyramide, Seitenflächenhöhe und Oberflächeninhalt

Lösungsansatz über Forneln:

Oberfläche: O =  a * (a + ha x 2)
Körperhöhe:
h² =  ha² - (a/2)²    oder h² = s² - (d/2)²  wobei d = a * √2
Seitenflächenhöhe:
ha² =  h² + (a/2)²   

1. Körperhöhe ermitteln
h² = s² - (a*√2/2)² 
h = √(s² - (a*√2/2)²  )
h = √(20² - (15*√2/2)²  )≈ √(20²-112,5) ≈17 cm

2. Seitenflächenhöhe ermitteln
ha² =  h² + (a/2)²= 17² +(15/2)²
ha = √(17² +(15/2)²)≈ 18,6 cm

3. Oberfläche ermitteln
O =  a * (a + ha x 2)
O = 15*(15 + 18,6*2)
O ≈ 783 cm²