eine gute Freundin hat mich um etwas Hilfe gebeten. Sie kommt mit der Aufgabe zu einem Elektronikkonzern nicht gut klar bzw. sie weiß nicht wie sie vorgehen muss. Daher habe ich mir zu den Aufgaben, die auf den Bildern zu erkennen ist, Gedanken gemacht. Zur Vereinfachung habe ich mir ein Baumdiagramm (siehe Anhang) erstellt. Die Lösungen sind vorhanden. Ich kann mir das selbst irgendwie auch zusammenreimen. Vom Prinzip her verstehe ich die Aufgabe. Nur ich muss ihr das verständlich rüberbringen und das fällt mir schwer.
Kann mir bitte jemand stichpunktartig beschreiben, wie ich ihr die fünf einzelnen Aufgaben jeweils erläutern soll, damit sie das direkt versteht und selbst anwenden kann? Insbesondere bei b) kann ich die Umstellung des Verknüpfungssymbols nicht verstehen. Wieso dreht sich das um das eine ist eine oder- und das andere eine und-Verknüpfung oder?
Vielen lieben Dank
Aufgabenstellung
Text erkannt:
Aufgabe 1 (9 Punkte) Ein Elektronikkonzern stellt Mikrochips her. Dabei sind 20 Prozent der produzierten Chips defekt. Ein Prüfgerät entscheidet, ob ein Chip aussortiert oder verkauft wird. Das Gerät sortiert 94 Prozent aller defekten Chips aus, leider aber auch 7 Prozent aller intakten Chips. Sei \( D \) das Ereignis, dass ein zufállig ausgewählter Chip defekt ist und \( A \) das Ereignis, dass ein zufallig ausgewählter Chip aussortiert wird.
a) Bestimmen Sie die Wahrscheinlichkeit, dass ein zufallig ausgewählter Chip defekt ist und aussortiert wird.
Gegeben sind \( P(D)=0.2, P(A \mid D)=0.94 \) und \( P(A \mid \bar{D})=0.07 . \) Gesucht ist \( P(A \cap D) . \) Mit dem Multiplikationssatz erhält man
$$ P(A \cap D)=P(D) \cdot P(A \mid D)=0.2 \cdot 0.94=0.188 $$
Die gesuchte Wahrscheinlichkeit ist
b) Bestimmen Sie die Wahrscheinlichkeit \( P(\bar{A} \cup \bar{D}) \).
Hier ist gerade die Komplementarwahrscheinlichkeit zu Teil a) zu berechnen. Daher ist
$$ P(\bar{A} \cup \bar{D})=P(\overline{A \cap D})=1-P(A \cap D)=1-0.188=0.812 $$
Die gesuchte Wahrscheinlichkeit ist 0.812
:
Text erkannt:
c) Bestimmen Sie die Wahrscheinlichkeit, dass ein zufällig ausgewählter Chip aussortiert wird.
Mit dem Satz von der totalen Wahrscheinlichkeit erhält man
$$ P(A)=P(A \mid D) P(D)+P(A \mid \bar{D}) P(\bar{D})=0.94 \cdot 0.2+0.07 \cdot 0.8=0.244 $$
Die gesuchte Wahrscheinlichkeit ist 0.244
$$ $$
d) Wie groß ist die Wahrscheinlichkeit, dass ein aussortierter Chip auch tatsächlich defekt ist?
Mit dem Satz von Bayes erhălt man
$$ P(D \mid A)=\frac{P(A \mid D) P(D)}{P(A \mid D) P(D)+P(A \mid \bar{D}) P(\bar{D})}=\frac{0.94 \cdot 0.2}{0.244}=0.7705 $$
Die gesuchte Wahrscheinlichkeit ist 0.7705
e) Für eine bessere Genauigkeit wird ein neues Prüfgerät eingesetzt, das wie das alte auch 94 Prozent aller defekten Chips aussortiert. Es wird festgestellt, dass 21 Prozent aller hergestellten Chips aussortiert werden. Bestimmen Sie die Wahrscheinlichkeit dafür, dass dieses neue Gerät einen nicht defekten Chip aussortiert.
Für das neue Prüfgerät ist \( P(A)=0.21 \) und \( P(A \mid \bar{D}) \) ist jetzt gesucht. Mit dem Satz von der totalen Wahrscheinlichkeit erhält man
$$ P(A)=P(A \mid D) P(D)+P(A \mid D) P(D) $$
Auflösen nach \( P(A \mid \bar{D}) \) ergibt
$$ P(A \mid \bar{D})=\frac{P(A)-P(A \mid D) P(D)}{P(\bar{D})}=\frac{0.21-0.94 \cdot 0.2}{0.8}=0.0275 $$
Die gesuchte Wahrscheinlichkeit ist 0.0275
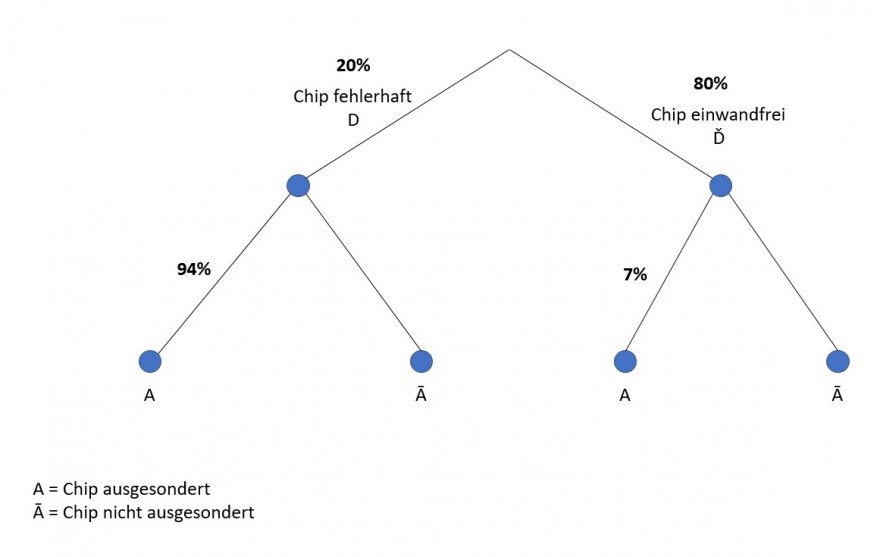
Text erkannt:
\( A= \) Chip ausgesondert
\( \overline{\mathrm{A}}= \) Chip nicht ausgesondert