Schließen von Grundgesamtheit auf Stichprobe, Sigmaregel: 3000-mal mit einem Laplacewürfel würfeln

Question

Aufgabe:

Schließen von der Grundgesamtheit auf die Stichprobe, Sigmaregel

a.) Sie würfeln 30- bzw. 300- bzw. 3000-mal mit einem Laplacewürfel. Erläutern Sie, wie viele "Sechser" Sie dabei erwarten. Nutzen Sie Intervalle für ihre Antworten.

b.) In welchem Intervall müsste die relative Häufigkeit der "niedrigen" Augenzahlen (1 bis 3) dabei mit ca. 95% Sicherheit liegen? Kommentieren Sie!


Problem/Ansatz:

Ich muss die oben geschilderte Aufgabe morgen im Unterricht präsentieren, um diese zu lösen, habe Ich zunächst 30:6, 300:6 und 3000:6 gerechnet. Aber schon bei diesem Schritt, wusste Ich nicht ob der überhaut notwendig ist und wie es dann weiter geht weiß Ich leider erst recht nicht



Falls jemand so lieb ist mir zu helfen, würde Ich mich über eine detaillierte Antwort freuen, damit Ich auch in der Lage bin die Aufgabe zu Präsentieren und die Schritte zu erklären

Comments

Brauchst du das denn noch immer?

Du hast ja schon einen ersten Schritt gemacht.

Was war hier das Ziel?

Wolltest du Wahrscheinlichkeiten ausrechnen? Erwartungswerte?

Und wenn ja, von was?

Answer 1

1) Sie würfeln 30- bzw. 300- bzw. 3000-mal mit einem Laplacewürfel. Erläutern Sie, wie viele "Sechser" Sie dabei erwarten. Nutzen Sie Intervalle für ihre Antworten.

Erwarten würdest du 30/6 = 5, 300/6 = 50 bzw 3000/6 = 500 Sechser. Das hast du völlig richtig gemacht.

Du sollst allerdings ein Intervall angeben. Nutze z.B. das 2-Sigma Intervall bei dem sich ca. 96% der Werte befinden.

I = [n·p - 2·√(n·p·(1 - p)), n·p + 2·√(n·p·(1 - p))]

Dann wären das die Intervalle

[1, 9] ; [37, 63] ; [459, 541]

Rechne das auf jeden Fall nochmal genau nach. Du solltest im Rahmen einer Präsentation auch genau auf die Sigma-Intervalle eingehen.

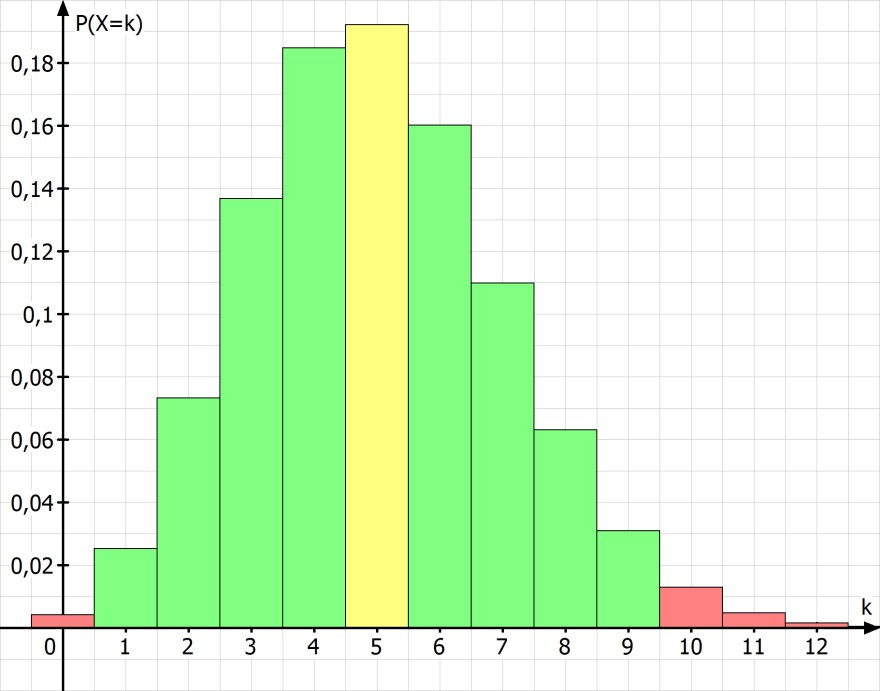
Man kann das dabei z.B. für n = 30 auch schön darstellen.