Hallo Rieki,
Mache Dir auf jeden Fall eine Skizze.
b) b= 6,0 cm Alpha=43,5 grad
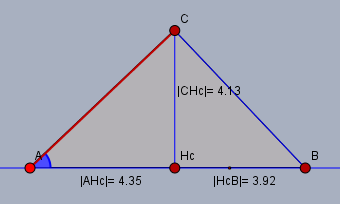
Stelle für den Winkel \(\alpha\) den Sinus im Dreieck \(\triangle AH_cC\) auf$$\sin \alpha = \frac hb$$Umstellen nach \(h\) liefert dann bereits$$h = b \cdot \sin \alpha = 6 \cdot \sin (43,5°) \approx 4,13$$\(q\) folgt aus dem Cosinus im Dreieck\(\triangle AH_cC\)$$\cos \alpha = \frac qb \\ q = b \cdot \cos \alpha = 6 \cdot \cos 43,5° \approx 4,35$$Und \(p\) kann man dann z.B. über den Höhensatz berechnen$$h^2 =pq \\ \begin{aligned}p &= \frac{h^2}q = \frac{\left( b \cdot \sin \alpha\right)^2}{b \cdot \cos \alpha} = b \cdot \tan \alpha \cdot \sin \alpha \\&= 6 \cdot \sin(43,5°) \cdot \tan(43,5°) \approx 3,92 \end{aligned}$$
c) a= 8,0 m Alpha= 28 grad
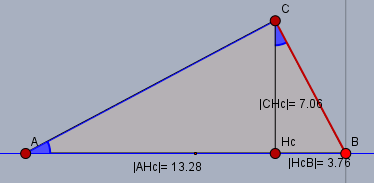
Den Winkel \(\alpha\) (blau) findest Du beim Punkt \(C\) wieder \(\angle H_cBC = \alpha\). Betrache das Dreieck \(\triangle H_cCB\)$$\cos \alpha = \frac {h_c}a \\ \implies h_c = a \cdot \cos \alpha = 8 \cdot \cos(28°) \approx 7,06$$Weiter gilt im Dreieck \(\triangle H_cBC\)$$\sin \alpha = \frac pa \\ \implies p = 8 \cdot \sin(28°) \approx 3,76$$und im Dreieck \(\triangle AH_cC\) kann man ablesen$$\tan \alpha = \frac{h_c}q \\ \implies q = \frac{h_c}{\tan \alpha} = \frac{7,06}{\tan(28°)} \approx 13,28$$
d) c= 12,0 cm Alpha= 72 grad
Du hast vielleicht gesehen, dass der 'Rechenweg' recht einfach ist. Es kommt vielmehr darauf an, den richtigen Zusammenhang zwischen drei Größen zu finden, von denen zwei gegeben sind.
Hier kannst Du mit dem Cosinus die Seite \(b\) berechnen. Und dann im Prinzip weiter wie oben.
e) c= 124,8 m Beta= 36 grad
Berechne mit dem Cosinus die Seite \(a\) und dann weiter wie beim Aufgabenteil b). Nur sind dann \(a\) und \(b\) und \(\alpha\) und \(beta\) vertauscht.
f) a= 65,4 m c= 54,7 m
Kathetensatz und Pythagoras führen hier sicher zum Ziel.
Falls Du noch Fragen hast, so melde Dich nochmal und stelle bitte konkrete Fragen.