Text erkannt:
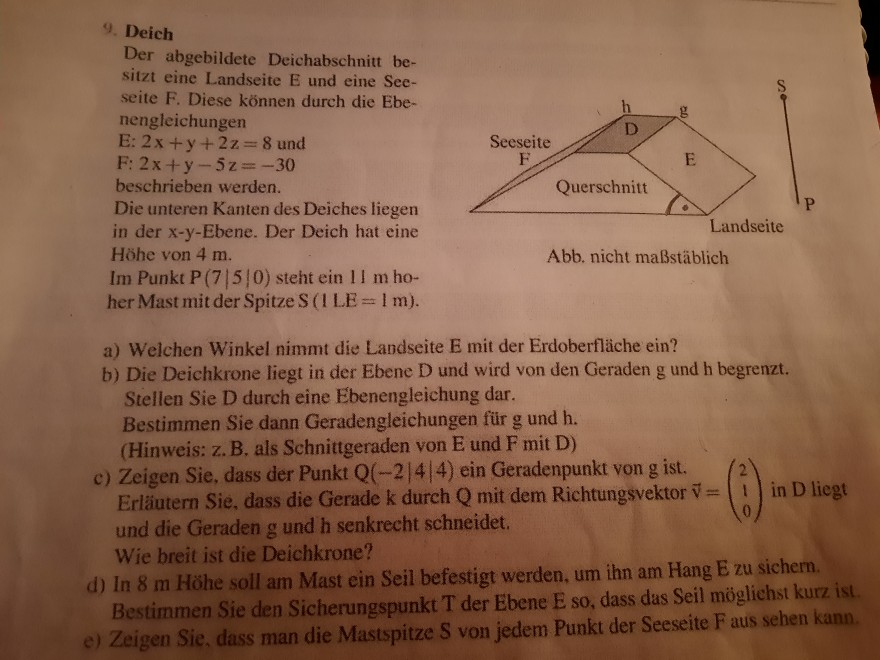
9. Deich Der abgebildete Deichabschnitt besitzt eine Landseite \( E \) und eine Seeseite F. Diese kơnnen durch die Ebenengleichungen
E: \( 2 x+y+2 z=8 \) und
\( F: 2 x+y-5 z=-30 \)
beschrieben werden. Die unteren Kanten des Deiches liegen in der \( x-y \) -Ebene. Der Deich hat eine Hóhe von \( 4 \mathrm{~m} . \quad \) Abb. nicht maßstäblich Im Punkt \( P(7|5| 0) \) steht ein \( 11 \mathrm{~m} \) hoher Mast mit der Spitze \( S(11 \mathrm{E}=1 \mathrm{~m}) \)
a) Welchen Winkel nimmt die Landseite \( \mathrm{E} \) mit der Erdoberfläche ein?
b) Die Deichkrone liegt in der Ebene \( \mathrm{D} \) und wird von den Geraden g und h begrenzt. Stellen Sie \( \mathrm{D} \) durch eine Ebenengleichung dar. Bestimmen Sie dann Geradengleichungen für \( g \) und \( h \). (Hinweis: \( \mathrm{Z} . \mathrm{B} \), als Schnittgeraden von Eund \( \mathrm{F} \) mit \( \mathrm{D} \) )
c) Zeigen Sie, dass der Punkt \( Q(-2) 4 \mid 4) \) ein Geradenpunkt von g ist. Erläutern Sie, dass die Gerade \( k \) durch \( Q \) mit dem Richtungsvektor \( v=\left(\begin{array}{l}2 \\ 1 \\ 0\end{array}\right) \) in \( D \) liegt und die Geraden g und h senkrecht schneidet. Wie breit ist die Deichkrone?
d) In \( 8 \mathrm{~m} \) Höhe soll am Mast ein Seil befestigt werden, um ihn am Hang E zu sichern. Bestimmen Sie den Sicherungspunkt T der Ebene E so, dass das Seil möglichst kurz isl.
e) Zeigen Sie, dass man die Mastspitze S von jedem Punkt der Seeseite F aus sehen kann.
Aufgabe:
wie berechne ich denn den Winkel zwischen der landseite E mit der Erdoberfläche ?
Liebe Grüße Martin