Bestimme den Konvergenzradius

Question

Aufgabe:

Bestimme den Konvergenzradius

\( \sum\limits_{n=0}^{\infty}{\frac{5^n}{n!}} \)

Problem/Ansatz:

Hallo könnte mir hier jemand erklären, wie man den Konvergenzradius bestimmt. Ich habe es mit der Regel von Hadamard versucht. Es ist mir aber nicht gelungen....

Answer 1

Aloah :)

Ich sehe nur eine Summe, die mich an die Potenzreihe der Exponentialfunktion erinnert:$$\sum\limits_{n=0}^\infty\frac{5^n}{n!}=e^5$$

Welchen Konvergenzradius möchtest du denn da bestimmen?

Comments

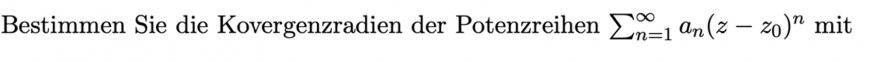
Text erkannt:

Bestimmen Sie die Konvergenzradien der Potenzreihen \( \sum \limits_{n=1}^{\infty} a_{n}\left(z-z_{0}\right)^{n} \) mit

Text erkannt:

(3) \( a_{n}=\frac{5^{n}}{n !} \).
\( R= \)

Das war die Aufgabenstellung.

Danke schonmal für die erste Hilfe !!

---

Ah, jetzt verstehe ich. Der Konvergenzradius ist der Grenzwert von

$$\frac{a_n}{a_{n+1}}=\frac{5^n}{n!}\cdot\frac{(n+1)!}{5^{n+1}}=\frac{5^n}{5^{n+1}}\cdot\frac{(n+1)!}{n!}=\frac{1}{5}\cdot(n+1)\to\infty$$Die Potenzreihe konvergiert also für alle \(z\in\mathbb R\).