Aufgabe:
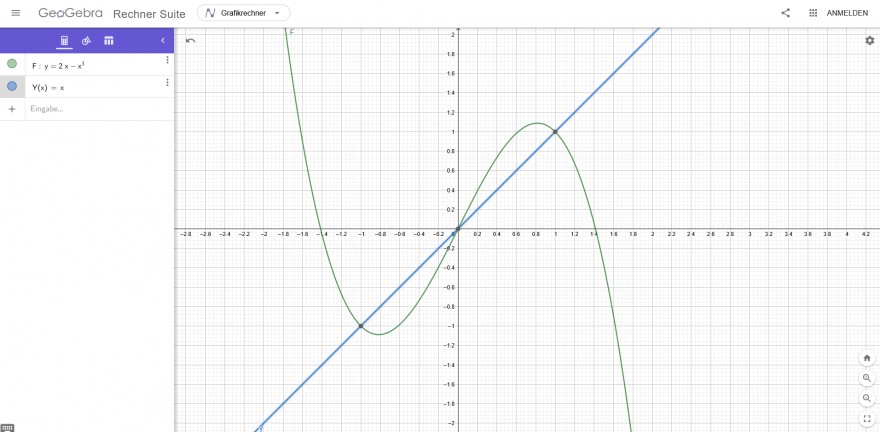
In welchem Verhältnis teilt die Gerade mit der Gleichung y=x die Fläche , die zwischen der Kurve mit der Gleichung y=2x-x^3 und der x-Achse im 1. Quadranten liegt?
Problem/Ansatz:
Y=x ist die erste WInkelhalbierende.
Die Nullstellen der Gleichung habe ich schon raus bekommen.Ich habe auch bereits den Integral von 0-1,4 berechnet. Mir ist sogar die Lösung bekannt (L:4/5)
Was ich allerdings nicht verstehe ist, wie man die Fläche zwischen der ersten Winkelhalbierenden und dem Graph im ersten Quadranten berechnet.
Ich habe was von Gleichsetzung der Funktionen gelsen, komme aber nicht weiter.
Ich hoffe es kann jemand helfen =).
Edit:
Ich habe nur einen Hauptschulabschluss und befinde mich momentan in der Oberstufe eines Abendgymnasiums.
Trotz Mathe schwächen bin ich im Mathe LK, weil es mir spaß macht =).
Mfg
Text erkannt:
GeoG