Baumdiagramm Lösung nicht nachvollziehbar

Question

Aufgabe:

Erstellen Sie ein Baumdiagramm zur Berechnung der Wahrscheinlichkeiten, dass von 2 zufällig ausgewählten deutschen Autos (s.o.), keines, eines oder genau zwei die Vorschrift (s.o.) erfüllt! Führen Sie diese Berechnung aus!

Lösung

Siehe Bild.

Problem/Ansatz:

Die Rechnung lautet 1/3*1/3+2/3*2/3.

Im übertragenen Sinne: genau Zwei oder keine der Autos führen eine Warnweste mit sich. Wo wird da Mitberechnet, dass nur ein Auto die Vorschrift erfüllt? Müsste dann nicht auch 1/3*2/3 dazugerechnet werden? Kann mir jemand erklären, wie ich das Ergebnis verstehen soll? Es ist für mich irgendwie nicht nachvollziehbar.

Text erkannt:

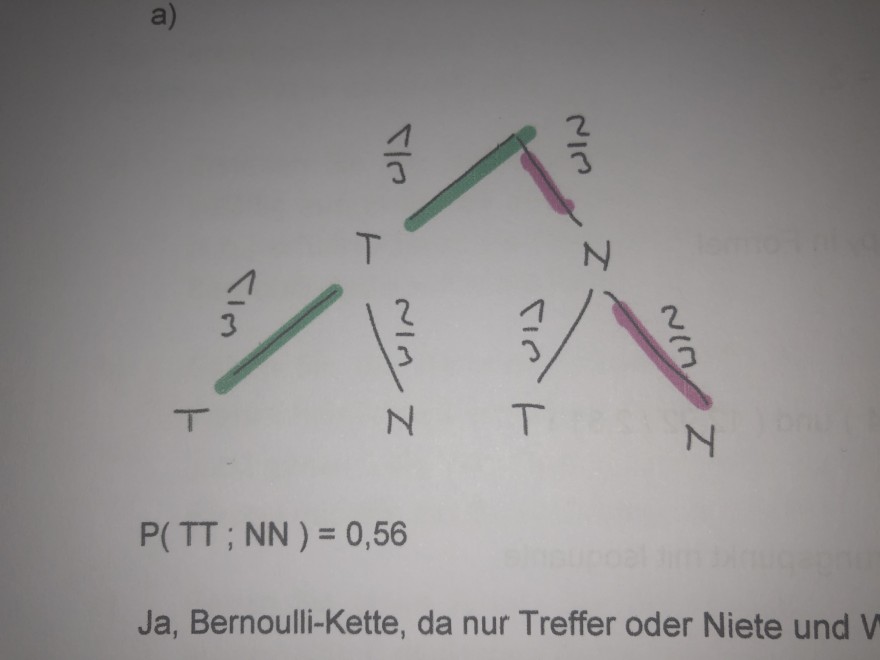
a)
\( P(T T ; N N)=0,56 \)
Ja, Bernoulli-Kette, da nur Treffer oder Niete und \( \mathrm{V} \)

Comments

Wie sind die Gegebenheiten
2/3 führen eine Warnweste mit
1/3 führt keine Warnweste mit ?

---

@georgborn

Das steht da nirgendwo in der Lösung aber ich gehe eigentlich davon aus, dass es anders herum ist, als wie Sie beschrieben haben. Ich kann es aber nicht genau sagen.

Answer 1

Ausgehend von
1/3 führen eine Warnweste mit
2/3 führt keine Warnweste mit

K Keine Warnweste 2/3
W Warnweste 1/3

Möglichkeiten für 2 Autos
K K 2/3 * 2/3 = 4/9
W W 1/3 * 1/3 = 1 / 9
W K 1/3 * 2/3 =2/9
K W 2/3 * 1/3 = 2/9

Zusammen 9/9

keines, 4/9
eines 2/9 * 2/9 = 4/9
genau zwei 1/9