Hi Tobi,
der Scheitelpunkt liegt bei S(2|2) was man leicht durch die Umformung:
y = x^2-4x+6 = x^2-4x+4+2 = (x-2)^2+2
sehen kann.
Nun geht die Gerade g durch diesen Scheitelpunkt und hat die Steigung m = 1/2.
Folglich muss die Gerade g: y = 1/2*x + 1 lauten, denn für x = 2 geht g in der Tat durch S(2|2).
Wenn nun eine weitere Gerade senkrecht auf g stehen soll, so muss diese Gerade h die Steigung m = -2 besitzen. Außerdem muss sie durch P(0|6) gehen, also den Schnittpunkt der Parabel mit der y-Achse.
h: y = -2*x+6
wäre folglich diese Gerade. Tatsächlich geht die für x = 2 durch den Scheitelpunkt und erfüllt damit das Kriterium der Orthogonalität, sowie die anderen gestellten Bedingungen.
Flächeninhalt errechnet sich über A = h*g, wobei h und g die jeweils relevanten Abschnitter der jeweiligen Geraden sind.
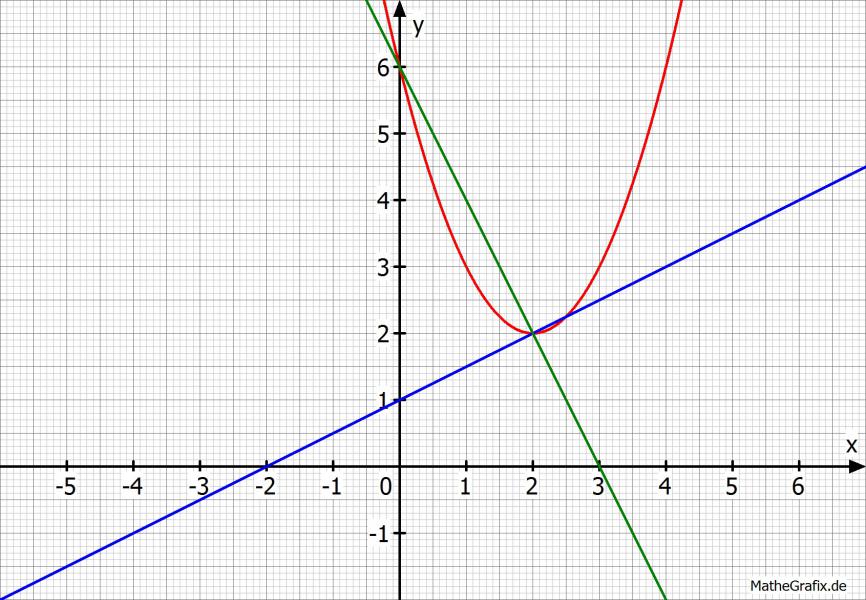
Im Schaubild sieht man super gut, dass man da mit dem Pythagoras ansetzen kann.
Für g^2 = 1^2+2^2 --> g = √5 (blaue Gerade)
Für h^2 = 4^2+2^2 --> h = √20 (grüne Gerade)
Also A = √5*√20 = √100 = 10
Der Flächeninhalt hat also eine Fläche von A = 10 FE.
Grüße