Question

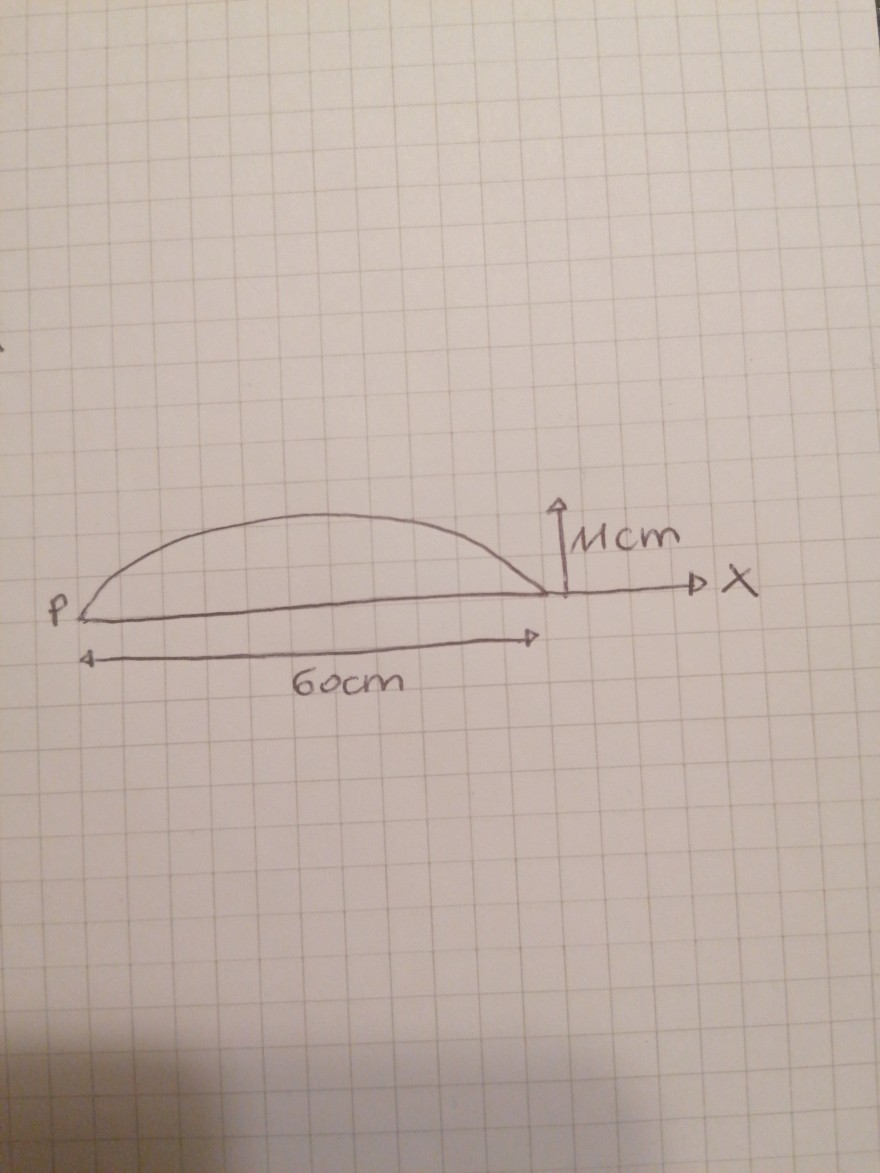
Die obere Abschlusskante der dargstellten Sessellehne ist parabelförmig.

Ermittle die gleichung wenn:

a) Der Koordinatenursprung im Scheitel liegt.

b) die x Achse auf der untern Linie liegt und die y-Achse die Symmetrieachse ist.

c)  Der Koordinatenursprung im Punkt P liegt

d) Beschreibe die Unterschiede zwischen den Funktionsgraphen.

Answer 1

Ermittle die gleichung

Funktionsgleichungen können anhand eines Graphen wie folgt ermittelt werden:

1. Punkte aus Graph ablesen
2. Punkte in allgemeine Funktionsgleichung einsetzen
3. Gleichungssystem lösen um die Parameter zu bestimmen
4. Parameter in Funktionsgleichung einsetzen

Die obere Abschlusskante der dargstellten Sessellehne ist parabelförmig.

Allgemeine Funktionsgleichung lautet

        \(f(x) = ax^2 + bx + c\).

Es müssen die drei Parameter \(a\), \(b\) und \(c\) bestimmt werden.

Also benötigst du drei Punkte.

a) Der Koordinatenursprung im Scheitel liegt.

1. Punkte sind \((-30|-11)\), \((0|0)\) und \((30|-11)\).

2. Einsetzen liefert die Gleichungen
   

           \(\begin{aligned}-11 &= a\cdot (-30)^2 + b\cdot (-30) + c\\0 &= a\cdot 0^2 + b\cdot 0 + c\\-11 &= a\cdot 30^2 + b\cdot 30 + c\\\end{aligned}\)

3. Lösung des Gleichungssystems ist

           \(a = -\frac{11}{900},b=0,c=0\)
   

4. Einsetzen in die allgemeine Funktionsgleichung ergibt

           \(f(x) = -\frac{11}{900}x^2\)