Aufgabe:
Brauche Hilfe bei d) und e)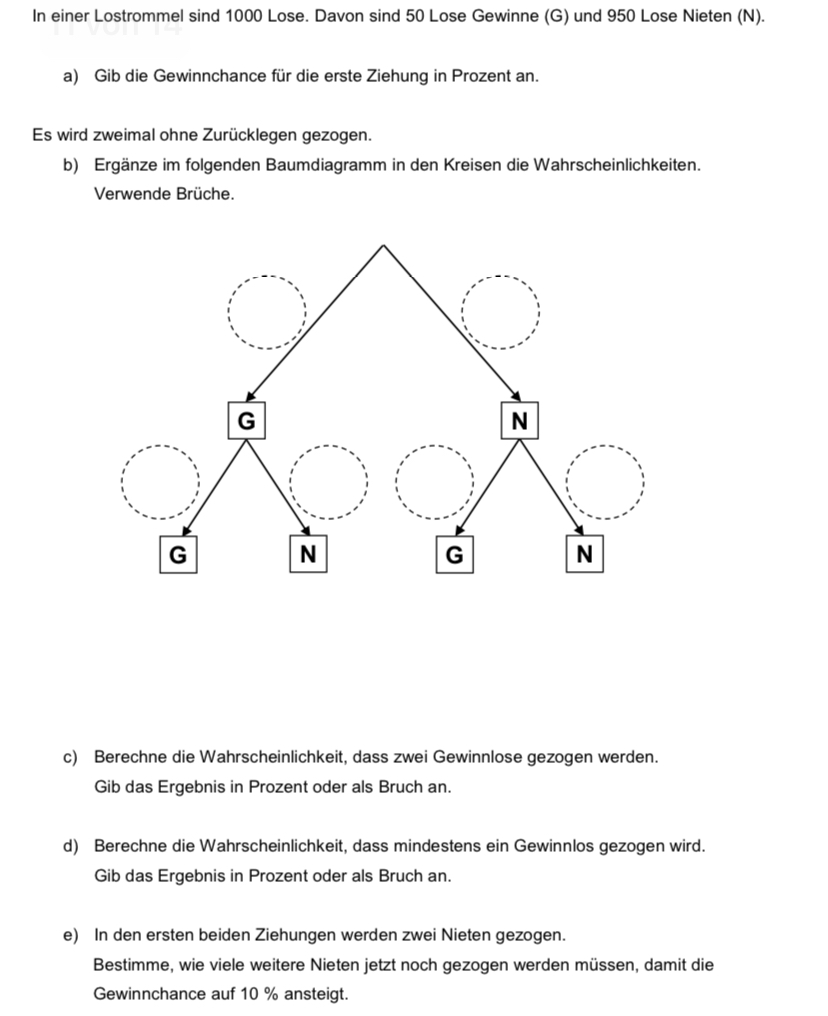
Text erkannt:
In einer Lostrommel sind 1000 Lose. Davon sind 50 Lose Gewinne (G) und 950 Lose Nieten (N).
a) Gib die Gewinnchance für die erste Ziehung in Prozent an.
Es wird zweimal ohne Zurücklegen gezogen.
b) Ergänze im folgenden Baumdiagramm in den Kreisen die Wahrscheinlichkeiten.
Verwende Brüche.
c) Berechne die Wahrscheinlichkeit, dass zwei Gewinnlose gezogen werden.
Gib das Ergebnis in Prozent oder als Bruch an.
d) Berechne die Wahrscheinlichkeit, dass mindestens ein Gewinnlos gezogen wird.
Gib das Ergebnis in Prozent oder als Bruch an.
e) In den ersten beiden Ziehungen werden zwei Nieten gezogen.
Bestimme, wie viele weitere Nieten jetzt noch gezogen werden müssen, damit die
Gewinnchance auf \( 10 \% \) ansteigt.