Text erkannt:
b) Ermitteln Sie die Extremstellen des Graphens (siehe oben Funktion) und deren Art mithilfe der zweiten Ableitungsfunktion von \( g \)
Extremstellen: \( g^{\prime}(x)=0 \)
\( \left(2-x^{2}\right) \cdot e^{-x}=0 \)
\( x_{1}=\sqrt{2} \) oder \( x_{2}=-\sqrt{2} \)
Art der Extremstellen:
\( f^{\prime} \cdot(x)=\frac{-2 x \cdot e^{x}-\left(2-x^{2}\right) \cdot e^{x}}{\left(e^{x}\right)^{2}}=\frac{-2 x-2+x^{2}}{e^{x}} \)
\( f^{\cdot}(\sqrt{2})=\frac{\left(-2 \cdot(\sqrt{2})-2+(\sqrt{2})^{2}\right)}{e^{\sqrt{2}}} \approx-0,68<0 \rightarrow \) Maximum
\( f^{\prime}(-\sqrt{2})=\frac{\left(-2 \cdot(-\sqrt{2})-2+(-\sqrt{2})^{2}\right)}{e^{-\sqrt{2}}} \approx 11,6>0 \rightarrow \) Minimum

Text erkannt:
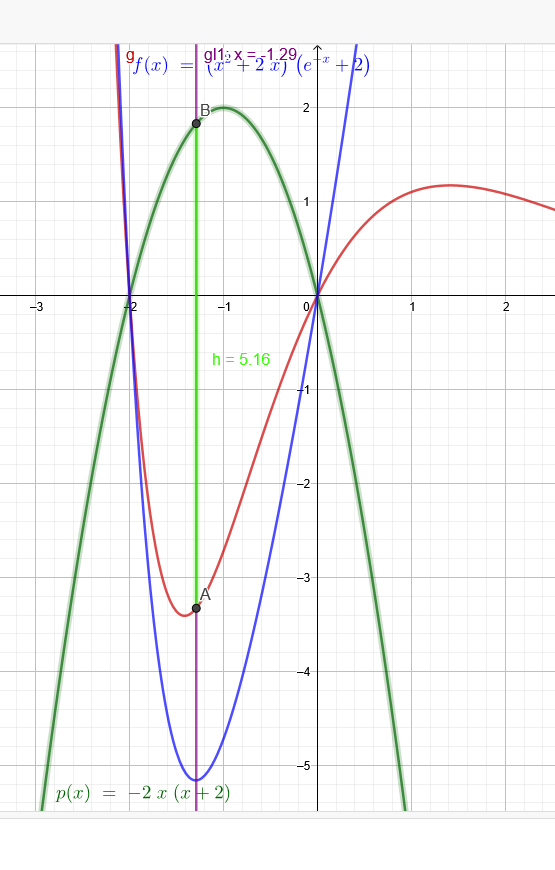
c) Der Graph \( p(x)=-2 x \cdot(x+2) \) und der Graph \( g(x)=\left(x^{2}+2 x\right) \cdot e^{-x} \) haben an genau einer Stelle \( x \) mit \( -2<x<0 \) einen maximalen senkrechten Abstand \( d \). Bestimmen Sie diese Stelle \( x \) und geben Sie den maximalen Abstand \( d \) an:
$$ \begin{array}{l} d(x)=\left(x^{2}+2 x\right) \cdot e^{-x}-[-2 x \cdot(x+2)]=\left(x^{2}+2 x\right) \cdot e^{-x}+2 x \cdot(x+2)=\left(x^{2}+2 x\right) \cdot e^{-x}+2 x^{2}+4 x= \\ =\left(x^{2}+2 x\right) \cdot e^{-x}+2 x^{2}+4 x=\left(x^{2}+2 x\right) \cdot e^{-x}+\left(x^{2}+2 x\right) \cdot 2=\left(x^{2}+2 x\right) \cdot\left(e^{-x}+2\right) \end{array} $$
\( \left[\left(x^{2}+2 x\right) \cdot\left(e^{-x}+2\right)\right]^{\prime}=0 \)
\( x \approx-1,29 \)
\( g(-1,29)=\left((-1,29)^{2}+2 \cdot(-1,29)\right) \cdot e^{-(-1,29)} \approx-3,33 \)
\( p(-1,29)=-2(-1,29) \cdot((-1,29)+2) \approx 1,8 \)
\( d=|-3,33|+1,8 \approx 5,13 \)