Text erkannt:
b) Ermitteln Sie die Extremstellen des Graphens (siehe oben Funktion) und deren Art mithilfe der zweiten Ableitungsfunktion von g
Extremstellen: g′(x)=0
(2−x2)⋅e−x=0
x1=2 oder x2=−2
Art der Extremstellen:
f′⋅(x)=(ex)2−2x⋅ex−(2−x2)⋅ex=ex−2x−2+x2
f⋅(2)=e2(−2⋅(2)−2+(2)2)≈−0,68<0→ Maximum
f′(−2)=e−2(−2⋅(−2)−2+(−2)2)≈11,6>0→ Minimum

Text erkannt:
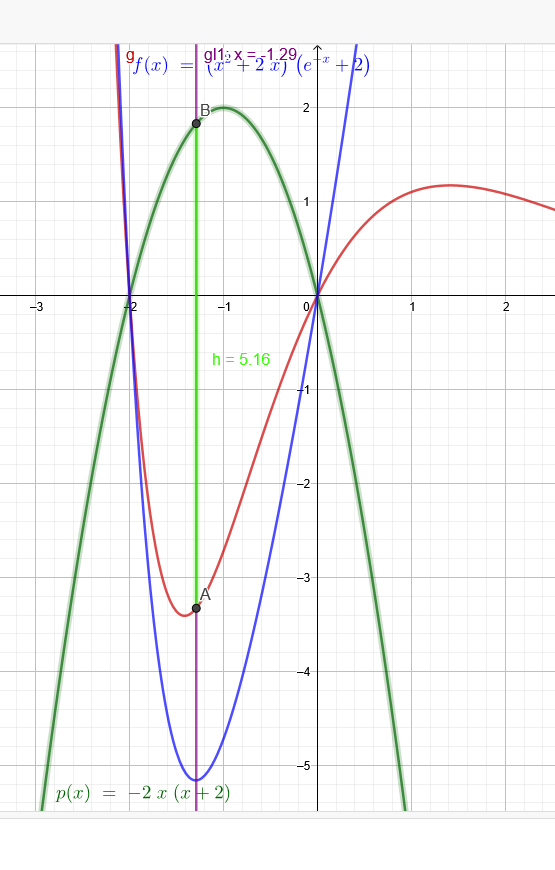
c) Der Graph p(x)=−2x⋅(x+2) und der Graph g(x)=(x2+2x)⋅e−x haben an genau einer Stelle x mit −2<x<0 einen maximalen senkrechten Abstand d. Bestimmen Sie diese Stelle x und geben Sie den maximalen Abstand d an:
d(x)=(x2+2x)⋅e−x−[−2x⋅(x+2)]=(x2+2x)⋅e−x+2x⋅(x+2)=(x2+2x)⋅e−x+2x2+4x==(x2+2x)⋅e−x+2x2+4x=(x2+2x)⋅e−x+(x2+2x)⋅2=(x2+2x)⋅(e−x+2)
[(x2+2x)⋅(e−x+2)]′=0
x≈−1,29
g(−1,29)=((−1,29)2+2⋅(−1,29))⋅e−(−1,29)≈−3,33
p(−1,29)=−2(−1,29)⋅((−1,29)+2)≈1,8
d=∣−3,33∣+1,8≈5,13