Wie hoch ist die mittlere Temperatur nach Mittag?

Question

Aufgabe:

Text erkannt:

Die Temperatur eines Tages verläuft nach folgender Gleichung:
$$ f(t)=18-\frac{1}{16}(t-12)^{2} $$
Dabei gibt \( f(t) \) die Temperatur in \( { }^{\circ} \mathrm{C} \) an und \( t \) die Zeit in Stunden, beginnend um 0 Uhr \( (t=0) \).
Wie hoch ist die mittlere Temperatur nach Mittag (zwischen 12 und 24 Uhr)?

Problem/Ansatz: Hi, ich hab so gerechnet: f (f) = 18t - 1/32 * (t-12)^3 ,dann habe ich einfach 24 und 12 eingesetzt, und erhalte 378 - 216 = 162 / 12 = 13,5

das richtige Ergebnis ist 15... sieht jemand einen Fehler? LG & Danke

Answer 1

Hallo,

berechne das Integral von 12 - 24 und teile das Ergebnis durch 12.

Gruß, Silvia

Answer 2

\( \frac{1}{12} \) ·\( \int\limits_{12}^{24} \)(18-\( \frac{1}{16} \)(t-12)²) dt=15.          

Answer 3

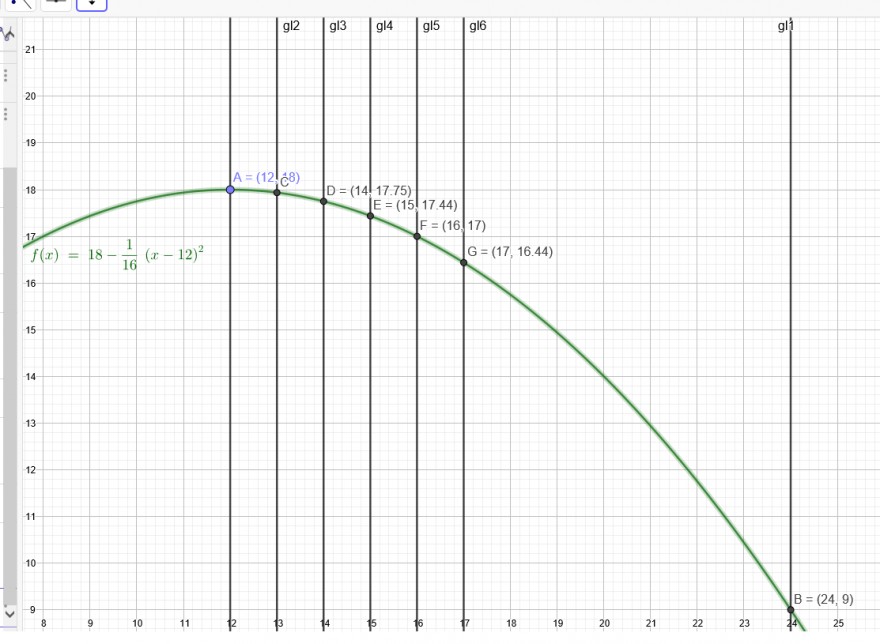
In der Zeichnung siehst du, wie du die Temperaturen zu jeder vollen Stunde herausbekommst:

12Uhr : f(12)=18-\( \frac{1}{16} \) (12-12)^2=18°

13Uhr:   f(13)=18-\( \frac{1}{16} \) (13-12)^2=...

14Uhr:   f(14)=18-\( \frac{1}{16} \) (14-12)^2=...

15Uhr:   f(15)=18-\( \frac{1}{16} \) (15-12)^2=...

.......................................................................

24Uhr:  f(24)=18-\( \frac{1}{16} \) (24-12)^2=...

Am Ende die 23 Temperaturwerte addieren und durch 23 dividieren.