Aufgabe:
Gegeben seien die beiden Graphen \( G_{1}=\left(V_{1}, E_{1}\right) \) und \( G_{2}=\left(V_{2}, E_{2}\right): \)
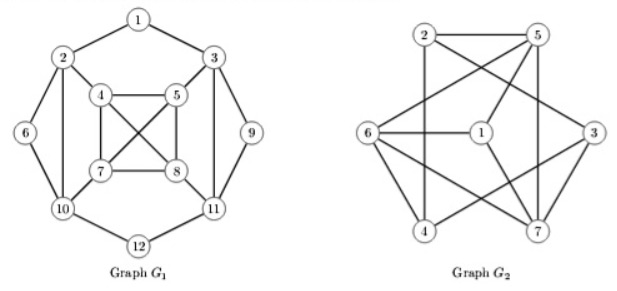
a) Entscheiden Sie, welcher der beiden Graphen \( G_{1} \) und \( G_{2} \) eine Eulertour besitzt. Geben Sie die entsprechende Eulertour an, oder beweisen Sie, dass keine existiert.
b) Besitzt der Graph \( G_{1} \) einen Hamiltonkreis? Begründen Sie Ihre Antwort.
c) Zeigen Sie, ob die Knotengrade des Graphen \( G_{2} \) die Bedingung (*) im Satz \( 3.19 \) von der Vorlesung erfüllen. Besitzt \( G_{2} \) trotzdem einen Hamiltonkreis? Begründen Sie Ihre Antwort.
Satz 3.19: Gilt in einem Graphen \( G=(V, E) \) die Bedingung: \( \operatorname{deg}(x)+\operatorname{deg}(y)>|V| \) für alle \( x, y \in V \) mit \( x \neq y \) und \( \{x, y\} \notin E \), so ist \( G \) hamiltonsch.
d) Entscheiden Sie, ob \( G_{1} \) und \( G_{2} \) planar sind. Begründen Sie Ihre Antwort.