Aufgabe:
Gegeben seien die beiden Graphen \( A \) und \( B \):
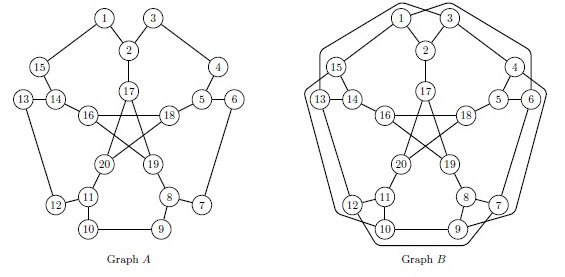
a) Entscheiden Sie, welcher der beiden Graphen \( A \) und \( B \) einen Hamiltonkreis besitzt. Geben Sie den entsprechenden Hamiltonkreis an, oder beweisen Sie, dass keiner exisitiert.
b) Zeigen Sie: Hat ein Graph einen Artikulationspunkt, also einen Knoten \( v \) so dass der Graph nach dem entfernen von \( v \) nicht mehr zusammenhängend ist, so hat der Graph keinen Hamiltonkreis.
c) Zeigen Sie allgemein: Zerfallt ein Graph nach dem Entfernen von \( k \) Knoten in mindestens \( k+1 \mathrm{Zu} \) sammenhangskomponenten, so enthält der Graph keinen Hamiltonkreis.