Hallo,
ich habe die Eigenwerte -1 und 3 raus und das Eigenwertproblem
(A-lamda E) * x = 0
alles richtig. Nun setze doch ein:$$\lambda = -1\space : \\ \begin{aligned}(A- \lambda E) \vec x &= \vec 0 \\ \left( \begin{pmatrix}1& 2\\ 2& 1\end{pmatrix} - (-1) \begin{pmatrix}1& 0\\ 0& 1\end{pmatrix}\right) \vec x &= \vec 0 \\ \begin{pmatrix}2& 2\\ 2& 2\end{pmatrix} \begin{pmatrix}x_1\\ x_2\end{pmatrix} &= \vec 0 \\ 2x_1 + 2x_2 &= 0 \\ \implies x_1 &= -x_2 \\ \implies e_{\lambda = -1} &= \begin{pmatrix}-1\\ 1\end{pmatrix} \end{aligned}$$eine der Koordinaten des Eigenvektors kannst Du frei wählen (z.B.: \(x_2=1\)). Eigenvektoren definieren sich nur über ihre Richtung.
Das gleiche machst Du für \(\lambda = 3\). Das resultiert in$$\lambda = 3\space :\\\begin{aligned} \begin{pmatrix}-2& 2\\ 2& -2\end{pmatrix} \begin{pmatrix}x_1\\ x_2\end{pmatrix} &= \vec 0 \\ \implies x_1 &= x_2 \\ e_{\lambda=3} &= \begin{pmatrix}1\\ 1\end{pmatrix} \end{aligned}$$Nachrechnen lassen kannst Du das auch hier.
Zur Erläuterung: Eigenvektoren sind Vektoren, die durch die Abbildung $$A \cdot e \to e'$$in ihrer Richtung nicht verändert werden. Der zugehörige Eigenwert gibt den Faktor der Längenänderung an.
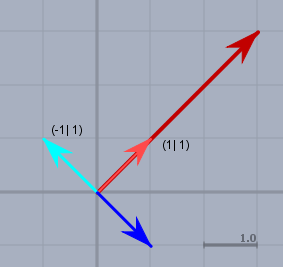
Oben im Bild wird der hellblaue Vektor \(e_{(-1)} = (-1|\,1)\) auf den blauen Vektor abgebildet$$\begin{pmatrix}1& 2\\ 2& 1\end{pmatrix} \cdot \begin{pmatrix}-1\\ 1\end{pmatrix} = \begin{pmatrix} 1\\ -1\end{pmatrix}$$\(e_{(-1)}\) behält die Richtung bei, wird aber mit dem Faktor \(\lambda_1=-1\) multipliziert. In gleicher Weise wird der hellrote Vektor \(e_{(3)}=(1|\,1)\) auf den roten abgebildet$$\begin{pmatrix}1& 2\\ 2& 1\end{pmatrix} \cdot \begin{pmatrix}1\\ 1\end{pmatrix} = \begin{pmatrix}3\\ 3\end{pmatrix}$$die Abbildung verhält sich wie ein Multiplikation des Vektors mit \(\lambda_2=3\) ohne Richtungsänderung.