Aufgabe:
Sie werden in einem Unternehmen, eingestellt, um die Forecasting Abteilung zu unterstützen. Ihre Aufgabe ist es, vierteljährliche Prognosen für einen Artikel zu erstellen, der ein Niveau, eine Saisonalität und einen Trend aufweist. Das Unternehmen verfügt zwar über ein bestehendes Holt-Winter-Prognosemodell, aber niemand weiß, wie die Parameter (Alpha, Beta oder Gamma) lauten.
Sie wissen aber, dass die Nachfrage in jedem Quartal historisch gesehen dieser Verteilung folgt:
- Q1 (Januar bis März) = 60 % der durchschnittlichen vierteljährlichen Nachfrage
- Q2 (April bis Juni) = 80 % der durchschnittlichen Quartalsnachfrage
- Q3 (Juli bis September) = 140% des durchschnittlichen Quartalsbedarfs
- Q4 (Oktober bis Dezember) = 120 % des durchschnittlichen Quartalsbedarfs.
Sie haben gerade die Prognose Ende September (Ende 2021Q3) durchgeführt und haben die folgenden Schätzungen:
Für Niveau: a^2021Q3 = 1050 Einheiten
Für den Trend: b^2021Q3= 40,5 Einheiten pro Quartal
a) Wie lautet Ihre Prognose für die Nachfrage für 2021Q4?
b) Angenommen, die tatsächliche Nachfrage nach dem Artikel im Jahr 202114Q4 beträgt 1050 Einheiten. Was ist der kleinstmögliche Wert für Ihre Schätzung für das Niveau, a^2021Q4 ?
Problem/Ansatz:
Ich kenne die Formeln vom Holt Winter Model, diese können hier aber nicht angewendet werden da kein alpha beta und gamma gegeben ist. Zudem habe ich keine Ahnung wie ich F^(t) nur auf Basis der durchschnittlichen Quartalsnachfrage bestimmen soll.
Das Model hätte ich so aufgebaut. Aber irgendwie macht es keinen Sinn (1050+40,5)*1,2 zu rechnen um auf x^(t,t+1) zu kommen, da die Q4 Nachfrage 120% und Q3 140% ist und somit die 1050 höher als x^(t,t+1) sein müssten.
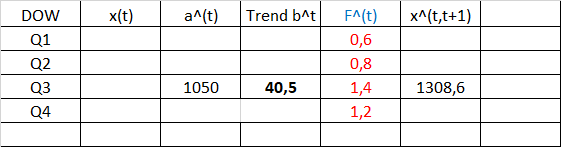
Hat jemand bessere Ideen oder kann mir irgendwie weiter helfen? :)