wie geht man sonst mit dieser Aufgabe um?

Question

Aufgabe:

Grenzwert bestimmen (mit L'Hospital)

Problem/Ansatz:

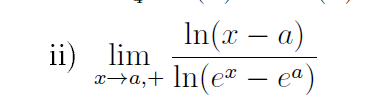
Text erkannt:

ii) \( \lim \limits_{x \rightarrow a,+} \frac{\ln (x-a)}{\ln \left(e^{x}-e^{a}\right)} \)

Ich komme der Lösung dieser Aufgabe leider nicht auf die Spur.

Wenn ich a einsetze dann erhalte ich doch 0 im ln und das ist mathematisch undefiniert.

wie geht man sonst mit dieser Aufgabe um?

Comments

\( \lim \limits_{x \rightarrow a} \frac{\ln (x-a)}{\ln \left(e^{x}-e^{a}\right)}=1 \)

Answer 1

Hallo

die Antwort steht doch schon in deiner Frage? L'Hopital, 2 mal anwenden.

Gruß lul

Comments

Mir war der schritt nicht bewusst bei mir hats am a+ gehackt aber habe vorhin gesehen wie man dabei vorgeht trotzdem danke!