f ( x ) = I x - 2 I < 2 + 2 * x
f ( x ) = I x - 2 I - 2 - 2 * x < 0
Die Lösungmenge ist wenn die Funktion < 0
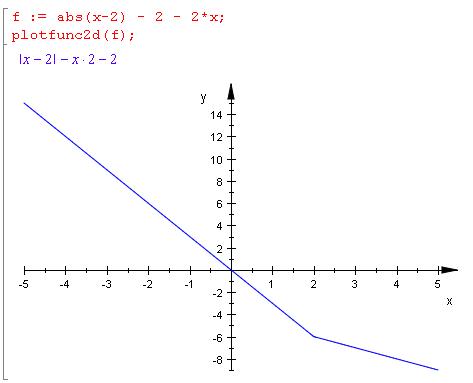
Rechnerisch
Fall 1: x - 2 > 0 => x > 2
und
x - 2 < 2 + 2 * x
x > -4
zusammen :
x > 2 und x > -4 => x > 2
Fall 2: x - 2 < 0 => x < 2
und
- ( x - 2 ) < 2 + 2 * x
-x + 2 < 2 + 2 * x
3 * x > 0
x > 0
zusammen :
x <2 und x > 0 => 0 < x < 2
Insgesamt Fall 1 und Fall 2
( x > 2 ) und ( 0 < x < 2 )
So. Jetzt kannst du dir noch ein paar Gedanken machen
wie es sich mit x = 2 verhält.
Dürfte aber mit zur Lösungsmenge gehören. Dann hätten wir
0 < x < ∞ ( siehe Skizze )
Bei Fehlern oder Fragen wieder melden.
mfg Georg