Schnittpunkt Funktionen Differenz

Question

Aufgabe:

Gegeben sind die Funktionen:

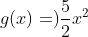
und h(x)=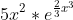

Es gilt (h(1)-g(1))*(h(2)-g(2))<0

Problem/Ansatz:

Diese Angabe soll begründen, dass sich die Graphen in dem Intervall 1-2mindestens 1mal schneiden, aber auf meinem Gtr schneiden sich nicht die Funktionen

Answer 1

Text erkannt:

\( g(x)=\frac{5}{2} x^{2} \)
\( h(x)=5 x^{2} \cdot e^{\frac{2}{3} x^{3}} \)
\( \frac{5}{2} x^{2}=5 x^{2} \cdot e^{\frac{2}{3} x^{3}} \mid \cdot \frac{2}{5} \)
\( x^{2}-2 x^{2} \cdot e^{\frac{2}{3} x^{3}}=0 \)
\( x^{2} \cdot\left(1-2 \cdot e^{\frac{2}{3} x^{3}}\right)=0 \)
\( x^{2}=0 \)
\( x_{1,2}=0 \rightarrow \rightarrow \) doppelte Nullstelle
\( \left(1-2 \cdot e^{\frac{2}{3} x^{3}}\right)=0 \)
\( e^{\frac{2}{3} x^{3}}=\frac{1}{2} \mid \ln \)
\( \frac{2}{3} x^{3}=\ln \left(\frac{1}{2}\right) \mid \cdot \frac{3}{2} \)
\( x^{3}=\frac{3}{2} \cdot \ln \left(\frac{1}{2}\right) \)
\( x=-\sqrt[3]{\frac{3}{2} \ln (2)} \rightarrow \rightarrow( \) mit Wolfram gefunden )