Berechnet den Flächeninhalt eurer Kreisringe.

Question

Ü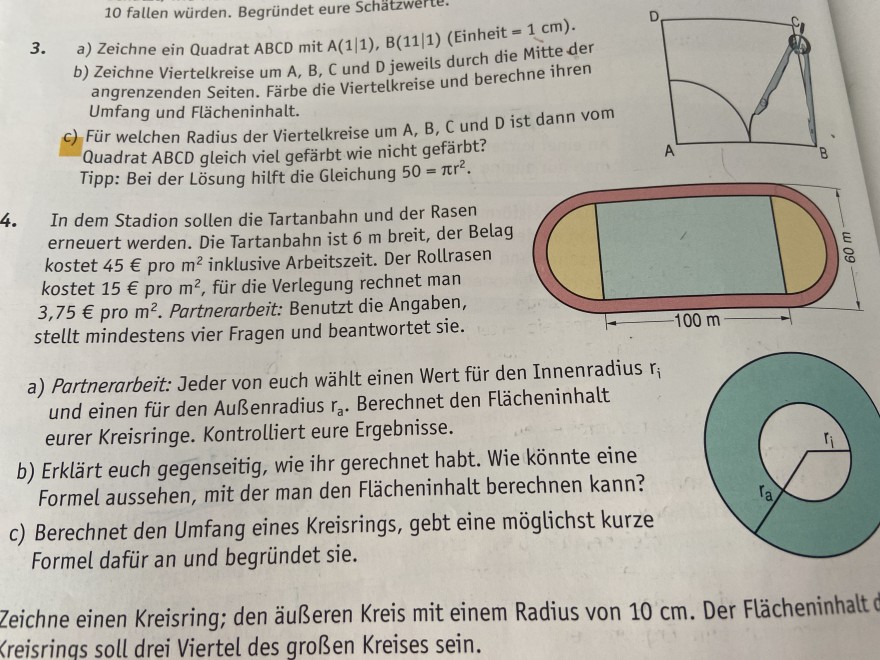

Text erkannt:

10 fallen würden. Beqründet
3. \( \quad \) a) Zeichne ein Quadrat \( \mathrm{ABCD} \) mit \( \mathrm{A}(1 \mid 1), \mathrm{B}(11 \mid 1) \) (Einheit = \( 1 \mathrm{~cm} \).
b) Zeichne Viertelkreise um \( \mathrm{A}, \mathrm{B}, \mathrm{C} \) und \( \mathrm{D} \) jeweils durch die Mitte der angrenzenden Seiten. Färbe die Viertelkreise und berechne ihren Umfang und Flächeninhalt.
c) Für welchen Radius der Viertelkreise um \( A, B, C \) und \( D \) ist dann vom Quadrat \( \mathrm{ABCD} \) gleich viel gefärbt wie nicht gefärbt? Tipp: Bei der Lösung hilft die Gleichung \( 50=\pi r^{2} \).
4. In dem Stadion sollen die Tartanbahn und der Rasen erneuert werden. Die Tartanbahn ist \( 6 \mathrm{~m} \) breit, der Belag kostet \( 45 € \) pro \( m^{2} \) inklusive Arbeitszeit. Der Rollrasen kostet \( 15 € \) pro \( \mathrm{m}^{2} \), für die Verlegung rechnet man \( 3,75 € \) pro \( m^{2} \). Partnerarbeit: Benutzt die Angaben, stellt mindestens vier Fragen und beantwortet sie.
a) Partnerarbeit: Jeder von euch wählt einen Wert für den Innenradius \( r_{i} \) und einen für den Außenradius \( r_{\mathrm{a}} . \) Berechnet den Flächeninhalt eurer Kreisringe. Kontrolliert eure Ergebnisse.
b) Erklärt euch gegenseitig, wie ihr gerechnet habt. Wie könnte eine Formel aussehen, mit der man den Flächeninhalt berechnen kann?
c) Berechnet den Umfang eines Kreisrings, gebt eine möglichst kurze Formel dafür an und begründet sie.
Zeichne einen Kreisring; den äußeren Kreis mit einem Radius von \( 10 \mathrm{~cm} \). Der Flächeninhalt \langlereisrings soll drei Viertel des großen Kreises sein.

Aufgabe:

Problem/Ansatz:

Text erkannt:

4. In dem Stadion sollen die Tartanbahn und der Rasen erneuert werden. Die Tartanbahn ist \( 6 \mathrm{~m} \) breit, der Belag kostet \( 45 € \) pro \( m^{2} \) inklusive Arbeitszeit. Der Rollrasen kostet \( 15 € \) pro \( \mathrm{m}^{2} \), für die Verlegung rechnet man \( 3,75 € \) pro \( m^{2} \). Partnerarbeit: Benutzt die Angaben, stellt mindestens vier Fragen und beantwortet sie.

Comments

Nur die Aufgabe 4 Bruch ich am besten auch mit Rechnung

Answer 1

Hallo

geht es um 3c)

dann ist die Gesamtfläche der 4 Viertelkreise gleich der Fläche eines ganzen Kreises mit dem Radius halbe Quadratseite.

 4) für die  Tartan-Bahn du hast insgesamt die geraden Stücken und zusammen einen Kreisring mit inneren Radius 30-6 und äusserem Radius 30, die geraden Stücke sind ja wohl klar?

das innere ist ein Rechteck mit Seitenlängen die du ablesen kannst und insgesamt ein ganzer Kreis mit Radius 24m.

bleibt dann noch ne Frage? Rechne soweit du kommst und frag nur bei Unsicherheiten nach

Gruß lul

Answer 2

Du hast bei der Tartanbahn 2 Halbkreise, der äußere jeweils mit dem Durchmesser 60, der Innere mit dem Durchmesser 60-(2*6), weil die Bahn ja 6 m breit ist. Dann rechnest du für beide Kreise die Fläche und ziehst den kleineren vom größeren ab. Dazu noch die Geraden: Länge 100, Breite 6. Damit hast du den Bedarf für die Tartanbahn.

Für den Rasen (ich nehme an, nur das grüne soll Rasen sein) brauchst du ja nur das Rechteck auszumessen, es ist 100m lang und 60-(2*6) m breit.

Danach die erhaltenen m² mal den Preisen (Verlegung nicht vergessen).