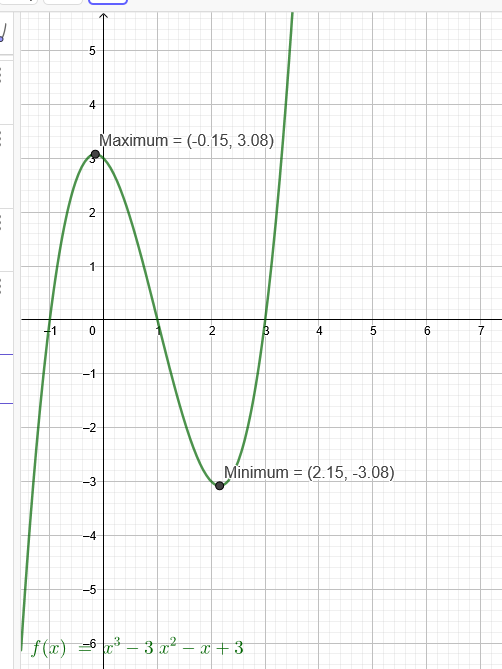
f(x)=x³-3x²-x+3
f´(x)=3x^2-6x-1
3x^2-6x-1=0
x^2-2x=\( \frac{1}{3} \)
(x-1)^2=\( \frac{1}{3} \)+1=\( \frac{4}{3} \)|\( \sqrt{} \)
1.) x-1=\( \frac{2}{3} \)\( \sqrt{3} \)
x₁=1+\( \frac{2}{3} \)\( \sqrt{3} \)≈2,2 y₁ =....
2.) x-1=-\( \frac{2}{3} \)\( \sqrt{3} \)
x₂=1-\( \frac{2}{3} \)\( \sqrt{3} \)≈-0,2 y₂ =....
f´´(x)=6x-6
f´´(2,2) = 6*2,2-6>0 → Minimum
f´´(-0,2) = 6*(-0,2)-6<0 →Maximum