Hallo Lia,
deine Angaben führen nicht zu einer eindeutigen Lösung. Da der abgebildete Funktionsgraph fehlt, kann mein Lösungsvorschlag eventuell nicht zur erwarteten Lösung passen.
Ich erläutere, wie ich auf den Ansatz
f(x)=-e^{kx}+c
komme.
e^x steigt. Da ein fallender Graph gesucht ist, setze ich ein Minuszeichen davor.
-e^x verläuft vollständig unterhalb der x-Achse. der Punkt (0|1) liegt aber oberhalb. Deshalb addiere ich c.
e^{-x}+c sieht prinzipiell schon gut aus, verläuft aber nicht durch (3|0). Also muss die Kurve noch "verbogen" werden. Das erreiche ich durch den Faktor k im Exponenten.
f(x)=-e^{kx}+c
(0|1) → 1=-1+c--> c=2
(3|0) → 0=-e^{k*3}+2
e^{k*3}=2
k*3=ln(2)
k=ln(2)/3
f(x)=-e^{x*ln(2)/3}+2
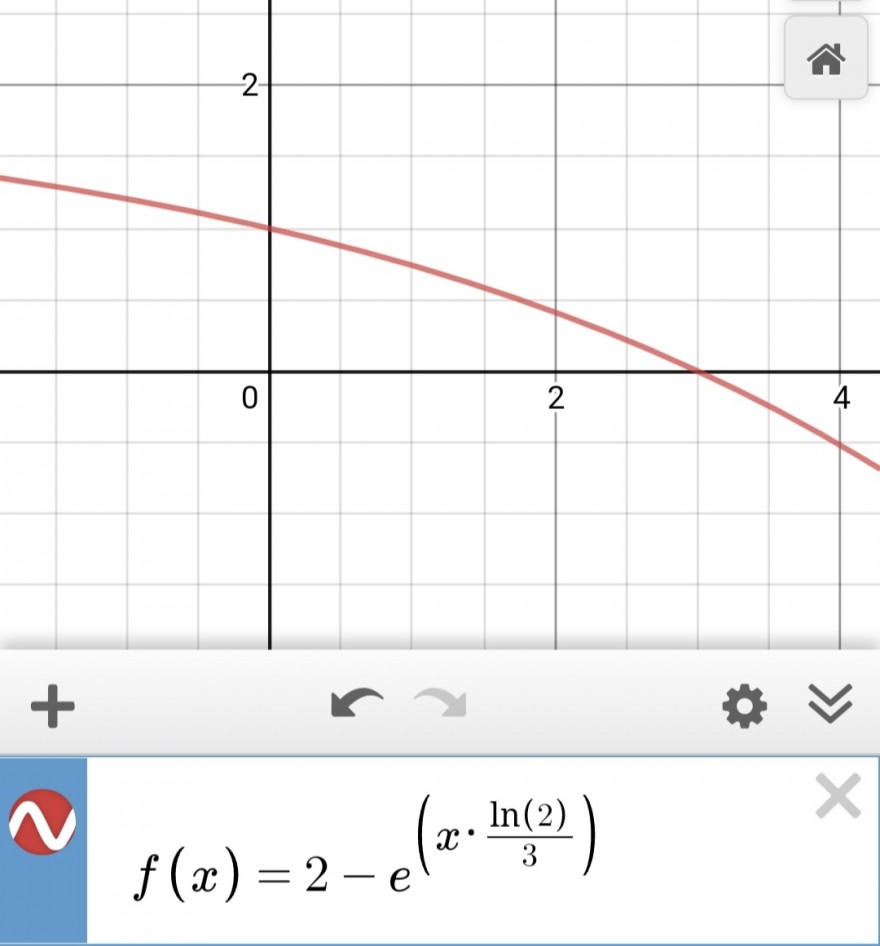
☺
PS:
Alternative Lösung:
f(x)=a*e^x+c
(0|1) → 1=a+c
(3|0) → 0=a*e^3 + c
Subtrahieren:
1=a*(1-e^3)
a=1/(1-e^3)
c=-a*e^3=-e^3 / (1-e^3)
f(x)=1/(1-e^3) *e^x -e^3/(1-e^3)
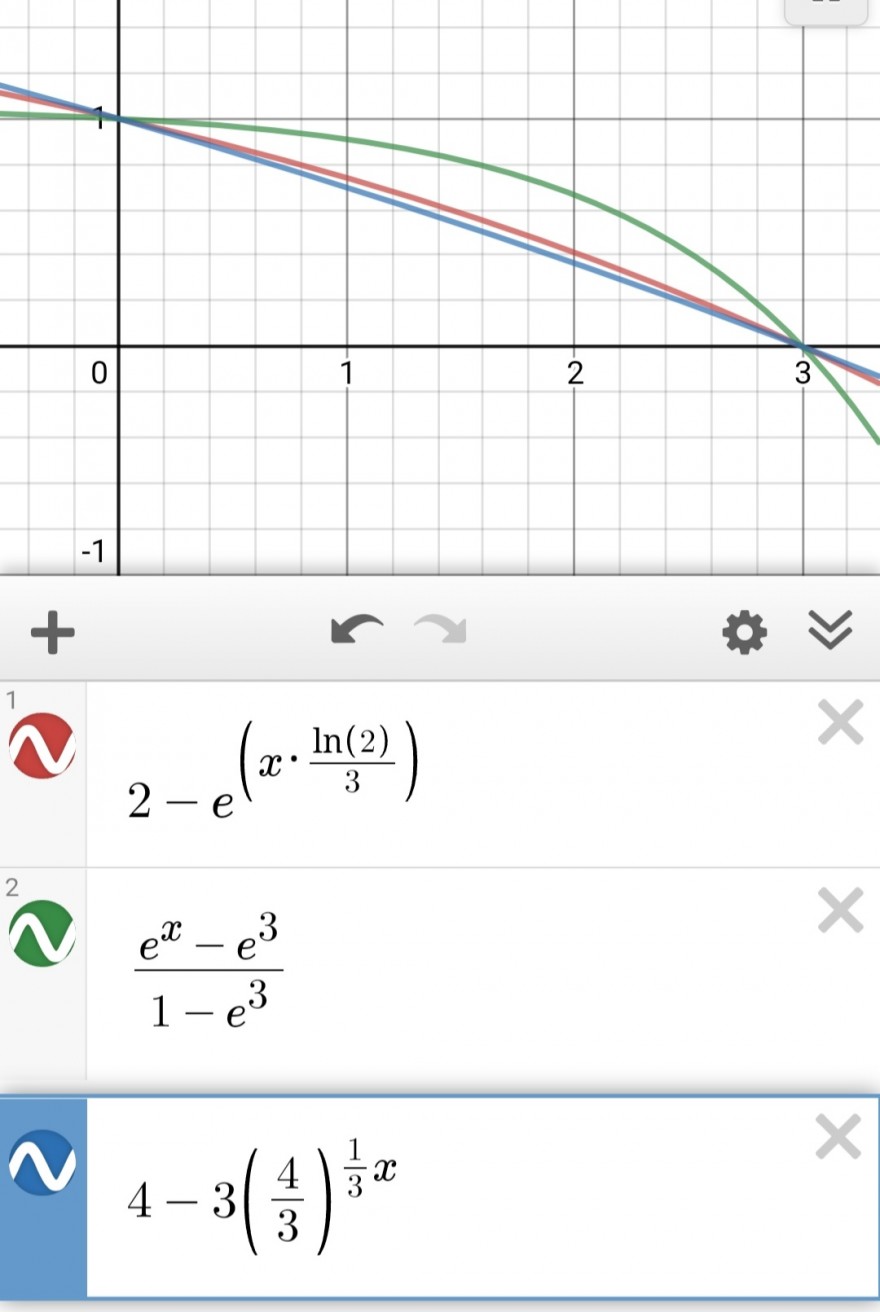
Du siehst hier drei von unendlich vielen Lösungen.
:-)