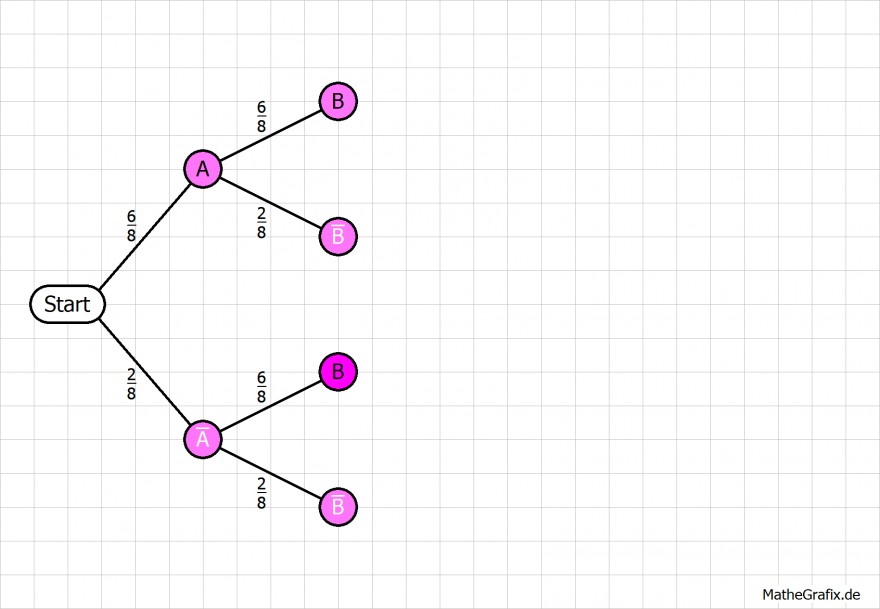
Du hast 6 grüne und 2 weiße Kugeln, d.h. die Wahrscheinlichkeiten für grün 6/8 und für weiß 2/8 (mit Zurücklegen.) Für die Wahrscheinlichkeit bei 2 Kugeln mußt du jetzt nur noch den jeweiligen Ast multiplizieren, also für "2 grüne" p=6/8*6/8
Für "mindestens 1 Weisse" ziehst du "keine weisse" von 1 ab - p(w>=1)= 1-p(kein w) = 1-p (2 grüne).
Bei 3 grünen und 1 weissen hättest du auf den Ästen die Wahrscheinlichkeiten von 3/4 bzw. 1/4. Rechne selbst weiter.
Ohne zurücklegen wären die 2. Äste (also die, die zu den B führen) nicht mehr 6/8, sondern für grün nach grün 5/7, für grün nach weiß 6/7 etc..