Bestimmen Sie die Wahrscheinlichkeit P(Y > = 127 / X=58)

Question

Aufgabe: Hallo, soll hier die Wahrscheinlichkeit von P(Y größer gleich 127 / x=58) bestimmen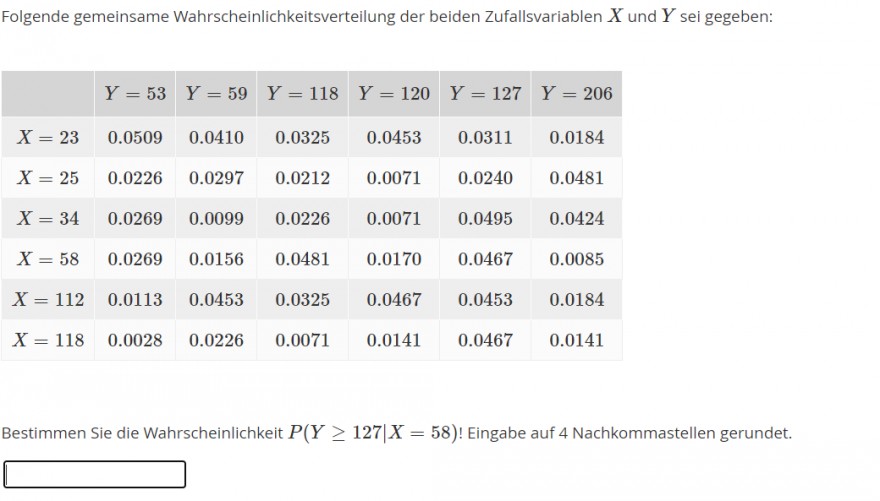

Text erkannt:

Folgende gemeinsame Wahrscheinlichkeitsverteilung der beiden Zufallsvariablen \( X \) und \( Y \) sei gegeben:
\begin{tabular}{ccccccc}
& \( Y=53 \) & \( Y=59 \) & \( Y=118 \) & \( Y=120 \) & \( Y=127 \) & \( Y=206 \) \\
\hline\( X=23 \) & \( 0.0509 \) & \( 0.0410 \) & \( 0.0325 \) & \( 0.0453 \) & \( 0.0311 \) & \( 0.0184 \) \\
\( X=25 \) & \( 0.0226 \) & \( 0.0297 \) & \( 0.0212 \) & \( 0.0071 \) & \( 0.0240 \) & \( 0.0481 \) \\
\( X=34 \) & \( 0.0269 \) & \( 0.0099 \) & \( 0.0226 \) & \( 0.0071 \) & \( 0.0495 \) & \( 0.0424 \) \\
\( X=58 \) & \( 0.0269 \) & \( 0.0156 \) & \( 0.0481 \) & \( 0.0170 \) & \( 0.0467 \) & \( 0.0085 \) \\
\( X=112 \) & \( 0.0113 \) & \( 0.0453 \) & \( 0.0325 \) & \( 0.0467 \) & \( 0.0453 \) & \( 0.0184 \) \\
\( X=118 \) & \( 0.0028 \) & \( 0.0226 \) & \( 0.0071 \) & \( 0.0141 \) & \( 0.0467 \) & \( 0.0141 \)
\end{tabular}
Bestimmen Sie die Wahrscheinlichkeit \( P(Y \geq 127 \mid X=58) ! \) Eingabe auf 4 Nachkommastellen gerundet.

Problem/Ansatz:

Ich habe mir gedacht es geht um die zwei Zahlen: 0.0467 und 0.0085 ich habe sie bereits addiert und multipliziert jedoch komme ich nicht auf die richtige Lösung. Hat jemand einen Rechenweg bzw. Lösung für mich? Vielen Dank im Voraus!!

Answer 1

es geht um die zwei Zahlen: 0.0467 und 0.0085

Addiere diese um \(P(Y\geq 127 ∧ X=58)\) zu berechnen.

Addiere die Zahlen der Zeile \(X=58\) um \(P(X=58)\) zu berechnen.

Teile das erste Ergebnis durch das zweite Ergebnis.

        \(P(A|B) = \frac{P(A\cap B)}{P(B)}\)

Comments

Vielen Dank:)