Hallo Harald,
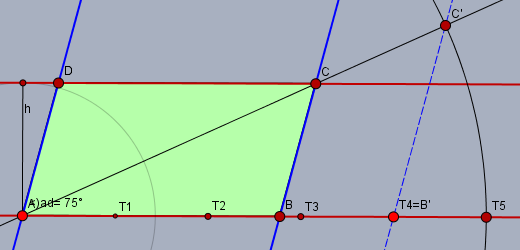
zeichne eine Gerade \(a\) (rot) und auf ihr einen Punkt \(A\). Trage in \(A\) den Winkel \(\alpha = 75°\) ab. Der Schenkel (blau) des Winkels sei \(d\). Zeichne eine Gerade \(c\) (rot) parallel zu \(a\) im Abstand von \(h= 3\,\text{cm}\) oberhalb von \(a\). Der Schnittpunkt von \(d\) und \(c\) ist \(D\).
Wähle einen beliebigen Punkt \(T_1\) auf \(a\) rechts von \(A\). Trage die Strecke \(|AT_1|\) noch viermal auf \(a\) ab. Du erhältst die Punkte \(T_2\) bis \(T_5\). Ich nenne den Punkt \(T_4=B'\). Nun gilt \(|AB'| \div |AT_5| = 4 \div 5\). Zeichne eine Parallele \(b'\) (blau gestrichelt) zu \(d\) durch \(B'\). Der Kreis um \(A\) mit Radius \(|AT_5|\) schneidet \(b'\) oberhalb von \(a\) in \(C'\).
Die Gerade durch \(AC'\) (schwarz) schneidet die Parallele \(c\) in \(C\). Die Parallele zu \(d\) durch \(C\) (blau) schneidet \(a\) in \(B\). Das Viereck \(ABCD\) ist das gesuchte Parallelogramm.
Gruß Werner