Hallo Chris,
Bitte verzweifelt um Hilfe :(
wo genau ist denn das Problem? Ist doch bloß einsetzen und ausrechnen. Ein Tabellenkalkulationsprogramm wäre hier übrigens hilfreich.
Substituiere zunächst einmal \(\dot\varphi(t) = \omega(t)\). Dann löst man die DGL nach \(\ddot\varphi(t)\) bzw. dann \(\dot\omega(t)\) auf, und erhält zwei Differentialgleichungen 1.Ordnung$$\dot \varphi(t) = \omega(t) \\ \dot\omega(t) = - \frac{k}{m} \omega(t) - \frac gl \sin(\varphi(t))$$Einsetzen der Zahlenwerte$$m = 110\,\text{kg} \\ l = 2\,\text m \\ k = 14\, \frac{\text{kg}}{\text s}\\ g = 9,81 \frac{\text m}{\text s^2}$$gibt für die zweite Gleichung$$\dot\omega(t) = - \frac{14\, \frac{\text{kg}}{\text s}}{110\,\text{kg}} \omega(t) - \frac {9,81 \frac{\text m}{\text s^2}}{2\,\text m } \sin(\varphi(t)) \\ \phantom{\dot\omega(t) } = - \frac{7}{55}\,\text s^{-1} \omega(t) - 4,95\,\text s^{-2}\sin(\varphi(t))$$und die Anfangsbedingung steht auch fest:$$\varphi(0) = 1, \quad \omega(0) =\dot\varphi(0)= -1\,\text s^{-1}$$Und weiter gilt nach dem Eulerverfahren$$\varphi(t + h) = \varphi(t) + \dot\varphi(t) \cdot h \\ \omega(t + h) = \omega(t) + \dot\omega(t) \cdot h$$Das alles in Form einer Tabelle ist$$\begin{array}{r|rrrr}t& \varphi(t)& \omega(t)& \dot\varphi(t)& \dot\omega(t)\\\hline 0& 1& -1& -1& -4.038009\\ 0.1& 0.9& -1.403801& -1.403801& -3.698803\\ 0.2& 0.759620& -1.773681& -1.773681& -3.183056\end{array}$$
hier mal beispielhaft der Verlauf von \(\varphi(t)\) über 2 Sekunden. Die blaue Kurve mit einem \(h=0,1\,\text s\) und die gelbe Kurve habe ich mit \(h=0,025\,\text s\) gerechnet.
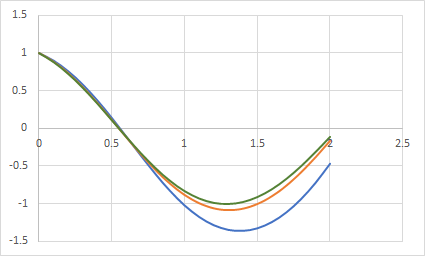
Die grüne Kurve ist mit einem Runge-Kutta-Verfahren gerechnet und kommt IMHO der Physik am nächsten.
Gruß Werner