Gerade im Raum g: x=a+r*m
a(ax/ay/az)=Stützpunkt (Stützvektor)
r=Geradenparameter,ist nur eine Zahl
m(mx/my/mz)=Richtungsvektor
Hinweis:Eine Gerade ist durch 2 Punkte A(ax/ay/az) und B(bx/by/bz) eindeutig bestimmt
A(ax/ay/az) → Ortsvektor a(ax/ay/az)
B(bx/by/bz) → Ortsvektor b(bx/by/bz)
Richtungsvektor m von Punkt A nach Punkt B → b=a+m → AB=m=b-a)
eingesetzt
Gerade g: x=(ax/ay/az)+rr*(b-a)
Infos
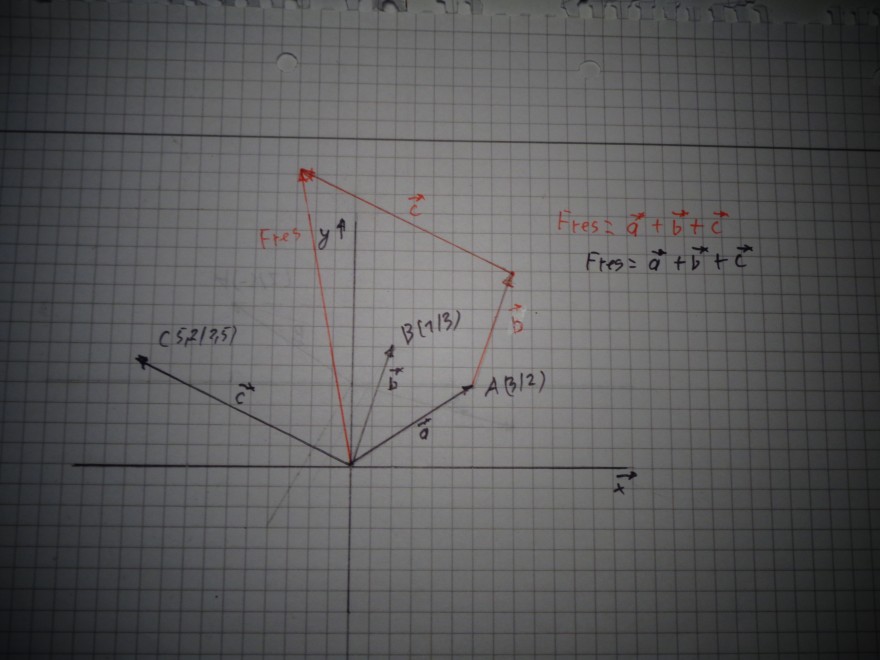
Text erkannt:
\( =a^{*}+\vec{b}+c \)
\( m=\vec{a}+\vec{b}+\vec{c} \)